Random Effects (in Mixed Model ANOVA). The term random effects in the context of analysis of variance is used to denote factors in an ANOVA design with levels that were not deliberately arranged by the experimenter (those factors are called fixed effects), but which were sampled from a population of possible samples instead. For example, if one were interested in the effect that the quality of different schools has on academic proficiency, one could select a sample of schools to estimate the amount of variance in academic proficiency (component of variance) that is attributable to differences between schools.

A simple criterion for deciding whether or not an effect in an experiment is random or fixed is to ask how one would select (or arrange) the levels for the respective factor in a replication of the study. For example, if one wanted to replicate the study described in this example, one would choose (take a sample of) different schools from the population of schools. Thus, the factor "school" in this study would be a random factor. In contrast, if one wanted to compare the academic performance of boys to girls in an experiment with a fixed factor Gender, one would always arrange two groups: boys and girls. Hence, in this case the same (and in this case only) levels of the factor Gender would be chosen when one wanted to replicate the study.

See also, Analysis of Variance and Variance Components and Mixed Model ANOVA/ANCOVA.

Range Plots - Boxes. In this style of range plot, the range is represented by a "box" (i.e., as a rectangular box where the top of the box is the upper range and the bottom of the box is the lower range). The midpoints are represented either as point markers or horizontal lines that "cut" the box.

Range Plots - Columns. In this style of range plot, a column represents the mid-point (i.e., the top of the column is at the mid- point value) and the range (represented by "whiskers") is overlaid in the column.

Range Plots - Whiskers. In this style of range plot (see example above), the range is represented by "whiskers" (i.e., as a line with a serif on both ends). The midpoints are represented by point markers.

Ratio Scale. This scale of measurement contains an absolute zero point, therefore it allows you to not only quantify and compare the sizes of differences between values, but also to interpret both values in terms of absolute measures of quantity or amount (e.g., time; 3 hours is not only 2 hours more than 1 hour, but it is also 3 times more than 1 hour).

See also, Measurement scales.

Rayleigh Distribution. The Rayleigh distribution has the probability density function:

f(x) = x/b² * e^{-(x 2/2b2)}
0 x <
b > 0

where
b     is the scale parameter
e     is the base of the natural logarithm, sometimes called Euler's e (2.71...)

See also, Process Analysis.

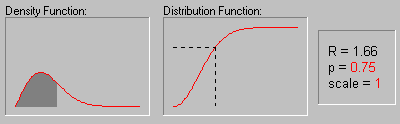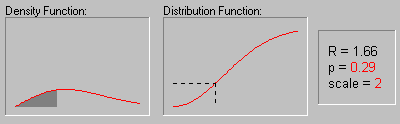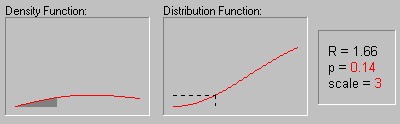
The graphic above shows the changing shape of the Rayleigh distribution when the scale parameter equals 1, 2, and 3.

Regression. A category of problems where the objective is to estimate the value of a continuous output variable from some input variables.

See also Multiple Regression.

Regular Histogram. This simple histogram will produce a column plot of the frequency distribution for the selected variable (if more than one variable is selected, then one graph will be produced for each variable in the list).

Regularization in Neural Networks. A modification to training algorithms which attempts to prevent over- or under-fitting of training data by building in a penalty factor for network complexity (typically by penalizing large weights, which correspond to networks modeling functions of high curvature) (Bishop, 1995).

See also Neural Networks.

Relative Function Change Criterion. The relative function change criterion is used to stop iteration when the function value is no longer changing (see Structural Equation Modeling). Basically, it stops iteration when the function ceases to change. The criterion is necessary because, sometimes, it is not possible to reduce the discrepancy function even when the gradient is not close to zero. This occurs, in particular, when one of the parameter estimates is at a boundary value. The "true minimum," where the gradient actually is zero, includes parameter values that are not permitted (like negative variances, or correlations greater than one).

On the i'th iteration, this criterion is equal to

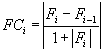
Reliability. There are two very different ways in which this term can be used:

Reliability and item analysis. In this context reliability is defined as the extent to which a measurement taken with multiple-item scale (e.g., questionnaire) reflects mostly the so-called true score of the dimension that is to be measured, relative to the error. A similar notion of scale reliability is sometimes used when assessing the accuracy (and reliability) of gages or scales used in quality control charting. For additional details refer to the Reliability and Item Analysis chapter, or the description of Gage Repeatability/Reproducibility Analysis in the Process Analysis chapter.

Weibull and reliability/failure time analysis. In this context reliability is defined as the function that describes the probability of failure (or death) of an item as a function of time. Thus, the reliability function (commonly denoted as R(t)) is the complement to the cumulative distribution function (i.e., R(t)=1-F(t)); the reliability function is also sometimes referred to as the survivorship or survival function (since it describes the probability of not failing or surviving until a certain time t; e.g., see Lee, 1992). For additional information, see Weibull and Reliability/Failure Time Analysis in the Process Analysis chapter.

Reliability and Item Analysis. In many areas of research, the precise measurement of hypothesized processes or variables (theoretical constructs) poses a challenge by itself. For example, in psychology, the precise measurement of personality variables or attitudes is usually a necessary first step before any theories of personality or attitudes can be considered. In general, in all social sciences, unreliable measurements of people's beliefs or intentions will obviously hamper efforts to predict their behavior. The issue of precision of measurement will also come up in applied research, whenever variables are difficult to observe. For example, reliable measurement of employee performance is usually a difficult task; yet, it is obviously a necessary precursor to any performance-based compensation system.

In all of these cases, Reliability & Item Analysis may be used to construct reliable measurement scales, to improve existing scales, and to evaluate the reliability of scales already in use. Specifically, Reliability & Item Analysis will aid in the design and evaluation of sum scales, that is, scales that are made up of multiple individual measurements (e.g., different items, repeated measurements, different measurement devices, etc.). Reliability & Item Analysis provides numerous statistics that allow the user to build and evaluate scales following the so-called classical testing theory model.

For more information, see the Reliability and Item Analysis chapter.

The term reliability used in industrial statistics denotes a function describing the probability of failure (as a function of time). For a discussion of the concept of reliability as applied to product quality (e.g., in industrial statistics), please refer to the section on Reliability/Failure Time Analysis in the Process Analysis chapter (see also the section Repeatability and Reproducibility in the same chapter and the chapter Survival/Failure Time Analysis). For a comparison between these two (very different) concepts of reliability, see Reliability.

Residual. Residuals are differences between the observed values and the corresponding values that are predicted by the model and thus they represent the variance that is not explained by the model. The better the fit of the model, the smaller the values of residuals. The ith residual (e_i) is equal to:

e_i = (y_i - y_i-hat)

where
y_i         is the ith observed value
y_i-hat   is the corresponding predicted value

See, Multiple Regression. See also, standard residual value, Mahalanobis distance, deleted residual and Cook’s distance.

Resolution. An experimental design of resolution R is one in which no l-way interactions are confounded with any other interaction of order less than R - l. For example, in a design of resolution R equal to 5, no l = 2-way interactions are confounded with any other interaction of order less than R - l = 3, so main effects are unconfounded with each other, main effects are unconfounded with 2-way interactions, and 2-way interactions are unconfounded with each other. For discussions of the role of resolution in experimental design see 2**(k-p) fractional factorial designs and 2**(k-p) Maximally Unconfounded and Minimum Aberration Designs.

Response Surface. A surface plotted in three dimensions, indicating the response of one or more variable (or a neural network) as two input variables are adjusted with the others held constant. See DOE, Neural Networks.

RMS (Root Mean Squared) Error. To calculate the RMS (root mean squared) error the individual errors are squared, added together, divided by the number of individual errors, and then square rooted. Gives a single number which summarizes the overall error. See Neural Networks.

Root Mean Square Standardized Effect (RMSSE). This standardized measure of effect size is used in the Analysis of Variance to characterize the overall level of population effects. It is the square root of the sum of squared standardized effects divided by the number of degrees of freedom for the effect. For example, in a 1-Way Anova, the RMSSE is calculated as

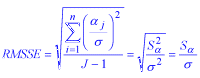
For more information see the chapter on Power Analysis.

Rosenbrock Pattern Search. This Nonlinear Estimation method will rotate the parameter space and align one axis with a ridge (this method is also called the method of rotating coordinates); all other axes will remain orthogonal to this axis. If the loss function is unimodal and has detectable ridges pointing towards the minimum of the function, then this method will proceed with a considerable accuracy towards the minimum of the function.

Runs Tests (in Quality Control). These tests are designed to detect patterns measurement (e.g., sample means) that may indicate that the process is out of control. In quality control charting, when a sample point (e.g., a mean in an X-bar chart) falls outside the control lines, one has reason to believe that the process may no longer be in control. In addition, one should look for systematic patterns of points (e.g., means) across samples, because such patterns may indicate that the process average has shifted. Most quality control software packages will (optionally) perform the standard set of tests for such patterns; these tests are also sometimes referred to as AT&T runs rules (see AT&T, 1959) or tests for special causes (e.g., see Nelson, 1984, 1985; Grant and Leavenworth, 1980; Shirland, 1993). The term special or assignable causes as opposed to chance or common causes was used by Shewhart to distinguish between a process that is in control, with variation due to random (chance) causes only, from a process that is out of control, with variation that is due to some non-chance or special (assignable) factors (cf. Montgomery, 1991, p. 102).

As the sigma control limits for quality control charts, the runs rules are based on "statistical" reasoning. For example, the probability of any sample mean in an X-bar control chart falling above the center line is equal to 0.5, provided (1) that the process is in control (i.e., that the center line value is equal to the population mean), (2) that consecutive sample means are independent (i.e., not auto-correlated), and (3) that the distribution of means follows the normal distribution. Simply stated, under those conditions there is a 50-50 chance that a mean will fall above or below the center line. Thus, the probability that two consecutive means will fall above the center line is equal to 0.5 times 0.5 = 0.25.

For additional information see Runs Tests; see also Assignable causes and actions.