This chapter includes a general introduction to ANOVA and a discussion of the general topics in the analysis of variance techniques, including repeated measures designs, ANCOVA, MANOVA, unbalanced and incomplete designs, contrast effects, post-hoc comparisons, assumptions, etc. For related topics, see also Variance Components (topics related to estimation of variance components in mixed model designs), Experimental Design/DOE (topics related to specialized applications of ANOVA in industrial settings), and Repeatability and Reproducibility Analysis (topics related to specialized designs for evaluating the reliability and precision of measurement systems).
See also General Linear Models, General Stepwise Regression; to analyze nonlinear models, see Generalized Linear Models.
The Purpose of Analysis of Variance
In general, the purpose of analysis of variance (ANOVA) is to test for significant differences between means. Elementary Concepts provides a brief introduction into the basics of statistical significance testing. If we are only comparing two means, then ANOVA will give the same results as the t test for independent samples (if we are comparing two different groups of cases or observations), or the t test for dependent samples (if we are comparing two variables in one set of cases or observations). If you are not familiar with those tests you may at this point want to "brush up" on your knowledge about those tests by reading Basic Statistics and Tables.
Why the name analysis of variance? It may seem odd to you that a procedure that compares means is called analysis of variance. However, this name is derived from the fact that in order to test for statistical significance between means, we are actually comparing (i.e., analyzing) variances.
For more introductory topics, see the topic name.See also Methods for Analysis of Variance, Variance Components and Mixed Model ANOVA/ANCOVA, and Experimental Design (DOE).
The Partioning of Sums of Squares
At the heart of ANOVA is the fact that variances can be divided up, that is, partitioned. Remember that the variance is computed as the sum of squared deviations from the overall mean, divided by n-1 (sample size minus one). Thus, given a certain n, the variance is a function of the sums of (deviation) squares, or SS for short. Partitioning of variance works as follows. Consider the following data set:
| Group 1 | Group 2 | |
|---|---|---|
| Observation 1 Observation 2 Observation 3 |
2 3 1 |
6 7 5 |
| Mean Sums of Squares (SS) |
2 2 |
6 2 |
| Overall Mean Total Sums of Squares |
4 28 |
|
| MAIN EFFECT | |||||
|---|---|---|---|---|---|
| SS | df | MS | F | p | |
| Effect Error |
24.0 4.0 |
1 4 |
24.0 1.0 |
24.0 |
.008 |
SS Error and SS Effect. The within-group variability (SS) is usually referred to as Error variance. This term denotes the fact that we cannot readily explain or account for it in the current design. However, the SS Effect we can explain. Namely, it is due to the differences in means between the groups. Put another way, group membership explains this variability because we know that it is due to the differences in means.
Significance testing. The basic idea of statistical significance testing is discussed in Elementary Concepts. Elementary Concepts also explains why very many statistical test represent ratios of explained to unexplained variability. ANOVA is a good example of this. Here, we base this test on a comparison of the variance due to the between- groups variability (called Mean Square Effect, or MSeffect) with the within- group variability (called Mean Square Error, or Mserror; this term was first used by Edgeworth, 1885). Under the null hypothesis (that there are no mean differences between groups in the population), we would still expect some minor random fluctuation in the means for the two groups when taking small samples (as in our example). Therefore, under the null hypothesis, the variance estimated based on within-group variability should be about the same as the variance due to between-groups variability. We can compare those two estimates of variance via the F test (see also F Distribution), which tests whether the ratio of the two variance estimates is significantly greater than 1. In our example above, that test is highly significant, and we would in fact conclude that the means for the two groups are significantly different from each other.
Summary of the basic logic of ANOVA. To summarize the discussion up to this point, the purpose of analysis of variance is to test differences in means (for groups or variables) for statistical significance. This is accomplished by analyzing the variance, that is, by partitioning the total variance into the component that is due to true random error (i.e., within- group SS) and the components that are due to differences between means. These latter variance components are then tested for statistical significance, and, if significant, we reject the null hypothesis of no differences between means, and accept the alternative hypothesis that the means (in the population) are different from each other.
Dependent and independent variables. The variables that are measured (e.g., a test score) are called dependent variables. The variables that are manipulated or controlled (e.g., a teaching method or some other criterion used to divide observations into groups that are compared) are called factors or independent variables. For more information on this important distinction, refer to Elementary Concepts.
Multi-Factor ANOVA
In the simple example above, it may have occurred to you that we could have simply computed a t test for independent samples to arrive at the same conclusion. And, indeed, we would get the identical result if we were to compare the two groups using this test. However, ANOVA is a much more flexible and powerful technique that can be applied to much more complex research issues.
Multiple factors. The world is complex and multivariate in nature, and instances when a single variable completely explains a phenomenon are rare. For example, when trying to explore how to grow a bigger tomato, we would need to consider factors that have to do with the plants' genetic makeup, soil conditions, lighting, temperature, etc. Thus, in a typical experiment, many factors are taken into account. One important reason for using ANOVA methods rather than multiple two-group studies analyzed via t tests is that the former method is more efficient, and with fewer observations we can gain more information. Let us expand on this statement.
Controlling for factors. Suppose that in the above two-group example we introduce another grouping factor, for example, Gender. Imagine that in each group we have 3 males and 3 females. We could summarize this design in a 2 by 2 table:
| Experimental Group 1 |
Experimental Group 2 |
|
|---|---|---|
| Males |
2 3 1 |
6 7 5 |
| Mean | 2 | 6 |
| Females |
4 5 3 |
8 9 7 |
| Mean | 4 | 8 |
Interaction Effects
There is another advantage of ANOVA over simple t-tests: ANOVA allows us to detect interaction effects between variables, and, therefore, to test more complex hypotheses about reality. Let us consider another example to illustrate this point. (The term interaction was first used by Fisher, 1926.)
Main effects, two-way interaction. Imagine that we have a sample of highly achievement-oriented students and another of achievement "avoiders." We now create two random halves in each sample, and give one half of each sample a challenging test, the other an easy test. We measure how hard the students work on the test. The means of this (fictitious) study are as follows:
| Achievement- oriented |
Achievement- avoiders |
|
|---|---|---|
| Challenging Test Easy Test |
10 5 |
5 10 |
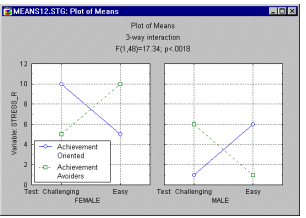
Higher order interactions. While the previous two-way interaction can be put into words relatively easily, higher order interactions are increasingly difficult to verbalize. Imagine that we had included factor Gender in the achievement study above, and we had obtained the following pattern of means:
| Females |
Achievement- oriented |
Achievement- avoiders |
|
|---|---|---|---|
| Challenging Test Easy Test |
10 5 |
5 10 |
|
| Males |
Achievement- oriented |
Achievement- avoiders |
|
| Challenging Test Easy Test |
1 6 |
6 1 |
|

Thus we may summarize this pattern by saying that for females there is a two-way interaction between achievement-orientation type and test difficulty: Achievement-oriented females work harder on challenging tests than on easy tests, achievement-avoiding females work harder on easy tests than on difficult tests. For males, this interaction is reversed. As you can see, the description of the interaction has become much more involved.
A general way to express interactions. A general way to express all interactions is to say that an effect is modified (qualified) by another effect. Let us try this with the two-way interaction above. The main effect for test difficulty is modified by achievement orientation. For the three-way interaction in the previous paragraph, we may summarize that the two-way interaction between test difficulty and achievement orientation is modified (qualified) by gender. If we have a four-way interaction, we may say that the three-way interaction is modified by the fourth variable, that is, that there are different types of interactions in the different levels of the fourth variable. As it turns out, in many areas of research five- or higher- way interactions are not that uncommon.
| To index |
Let us review the basic "building blocks" of complex designs.
For more introductory topics, click on the topic name.See also Methods for Analysis of Variance, Variance Components and Mixed Model ANOVA/ANCOVA, and Experimental Design (DOE).
Between-Groups and Repeated Measures
When we want to compare two groups, we would use the t test for independent samples; when we want to compare two variables given the same subjects (observations), we would use the t test for dependent samples. This distinction -- dependent and independent samples -- is important for ANOVA as well. Basically, if we have repeated measurements of the same variable (under different conditions or at different points in time) on the same subjects, then the factor is a repeated measures factor (also called a within-subjects factor, because to estimate its significance we compute the within-subjects SS). If we compare different groups of subjects (e.g., males and females; three strains of bacteria, etc.) then we refer to the factor as a between-groups factor. The computations of significance tests are different for these different types of factors; however, the logic of computations and interpretations is the same.
Between-within designs. In many instances, experiments call for the inclusion of between-groups and repeated measures factors. For example, we may measure math skills in male and female students (gender, a between-groups factor) at the beginning and the end of the semester. The two measurements on each student would constitute a within-subjects (repeated measures) factor. The interpretation of main effects and interactions is not affected by whether a factor is between-groups or repeated measures, and both factors may obviously interact with each other (e.g., females improve over the semester while males deteriorate).
Incomplete (Nested) Designs
There are instances where we may decide to ignore interaction effects. This happens when (1) we know that in the population the interaction effect is negligible, or (2) when a complete factorial design (this term was first introduced by Fisher, 1935a) cannot be used for economic reasons. Imagine a study where we want to evaluate the effect of four fuel additives on gas mileage. For our test, our company has provided us with four cars and four drivers. A complete factorial experiment, that is, one in which each combination of driver, additive, and car appears at least once, would require 4 x 4 x 4 = 64 individual test conditions (groups). However, we may not have the resources (time) to run all of these conditions; moreover, it seems unlikely that the type of driver would interact with the fuel additive to an extent that would be of practical relevance. Given these considerations, one could actually run a so-called Latin square design and "get away" with only 16 individual groups (the four additives are denoted by letters A, B, C, and D):
| Car | ||||
|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |
| Driver 1 Driver 2 Driver 3 Driver 4 |
A B C D |
B C D A |
C D A B |
D A B C |
Note that there are several other statistical procedures which may be used to analyze these types of designs; see the section on Methods for Analysis of Variance for details. In particular the methods discussed in the Variance Components and Mixed Model ANOVA/ANCOVA chapter are very efficient for analyzing designs with unbalanced nesting (when the nested factors have different numbers of levels within the levels of the factors in which they are nested), very large nested designs (e.g., with more than 200 levels overall), or hierarchically nested designs (with or without random factors).
| To index |
General Idea
The Basic Ideas section discussed briefly the idea of "controlling" for factors and how the inclusion of additional factors can reduce the error SS and increase the statistical power (sensitivity) of our design. This idea can be extended to continuous variables, and when such continuous variables are included as factors in the design they are called covariates.
For more introductory topics, see the topic name.See also Methods for Analysis of Variance, Variance Components and Mixed Model ANOVA/ANCOVA, and Experimental Design (DOE).
Fixed Covariates
Suppose that we want to compare the math skills of students who were randomly assigned to one of two alternative textbooks. Imagine that we also have data about the general intelligence (IQ) for each student in the study. We would suspect that general intelligence is related to math skills, and we can use this information to make our test more sensitive. Specifically, imagine that in each one of the two groups we can compute the correlation coefficient (see Basic Statistics and Tables) between IQ and math skills. Remember that once we have computed the correlation coefficient we can estimate the amount of variance in math skills that is accounted for by IQ, and the amount of (residual) variance that we cannot explain with IQ (refer also to Elementary Concepts and Basic Statistics and Tables). We may use this residual variance in the ANOVA as an estimate of the true error SS after controlling for IQ. If the correlation between IQ and math skills is substantial, then a large reduction in the error SS may be achieved.
Effect of a covariate on the F test. In the F test (see also F Distribution), to evaluate the statistical significance of between-groups differences, we compute the ratio of the between- groups variance (MSeffect) over the error variance (MSerror). If MSerror becomes smaller, due to the explanatory power of IQ, then the overall F value will become larger.
Multiple covariates. The logic described above for the case of a single covariate (IQ) can easily be extended to the case of multiple covariates. For example, in addition to IQ, we might include measures of motivation, spatial reasoning, etc., and instead of a simple correlation, compute the multiple correlation coefficient (see Multiple Regression).
When the F value gets smaller. In some studies with covariates it happens that the F value actually becomes smaller (less significant) after including covariates in the design. This is usually an indication that the covariates are not only correlated with the dependent variable (e.g., math skills), but also with the between-groups factors (e.g., the two different textbooks). For example, imagine that we measured IQ at the end of the semester, after the students in the different experimental groups had used the respective textbook for almost one year. It is possible that, even though students were initially randomly assigned to one of the two textbooks, the different books were so different that both math skills and IQ improved differentially in the two groups. In that case, the covariate will not only partition variance away from the error variance, but also from the variance due to the between- groups factor. Put another way, after controlling for the differences in IQ that were produced by the two textbooks, the math skills are not that different. Put in yet a third way, by "eliminating" the effects of IQ, we have inadvertently eliminated the true effect of the textbooks on students' math skills.
Adjusted means. When the latter case happens, that is, when the covariate is affected by the between-groups factor, then it is appropriate to compute so-called adjusted means. These are the means that one would get after removing all differences that can be accounted for by the covariate.
Interactions between covariates and factors. Just as we can test for interactions between factors, we can also test for the interactions between covariates and between-groups factors. Specifically, imagine that one of the textbooks is particularly suited for intelligent students, while the other actually bores those students but challenges the less intelligent ones. As a result, we may find a positive correlation in the first group (the more intelligent, the better the performance), but a zero or slightly negative correlation in the second group (the more intelligent the student, the less likely he or she is to acquire math skills from the particular textbook). In some older statistics textbooks this condition is discussed as a case where the assumptions for analysis of covariance are violated (see Assumptions and Effects of Violating Assumptions). However, because ANOVA/MANOVA uses a very general approach to analysis of covariance, you can specifically estimate the statistical significance of interactions between factors and covariates.
Changing Covariates
While fixed covariates are commonly discussed in textbooks on ANOVA, changing covariates are discussed less frequently. In general, when we have repeated measures, we are interested in testing the differences in repeated measurements on the same subjects. Thus we are actually interested in evaluating the significance of changes. If we have a covariate that is also measured at each point when the dependent variable is measured, then we can compute the correlation between the changes in the covariate and the changes in the dependent variable. For example, we could study math anxiety and math skills at the beginning and at the end of the semester. It would be interesting to see whether any changes in math anxiety over the semester correlate with changes in math skills.
| To index |
See also Methods for Analysis of Variance, Variance Components and Mixed Model ANOVA/ANCOVA, and Experimental Design (DOE).
Between-Groups Designs
All examples discussed so far have involved only one dependent variable. Even though the computations become increasingly complex, the logic and nature of the computations do not change when there is more than one dependent variable at a time. For example, we may conduct a study where we try two different textbooks, and we are interested in the students' improvements in math and physics. In that case, we have two dependent variables, and our hypothesis is that both together are affected by the difference in textbooks. We could now perform a multivariate analysis of variance (MANOVA) to test this hypothesis. Instead of a univariate F value, we would obtain a multivariate F value (Wilks' lambda) based on a comparison of the error variance/covariance matrix and the effect variance/covariance matrix. The "covariance" here is included because the two measures are probably correlated and we must take this correlation into account when performing the significance test. Obviously, if we were to take the same measure twice, then we would really not learn anything new. If we take a correlated measure, we gain some new information, but the new variable will also contain redundant information that is expressed in the covariance between the variables.
Interpreting results. If the overall multivariate test is significant, we conclude that the respective effect (e.g., textbook) is significant. However, our next question would of course be whether only math skills improved, only physics skills improved, or both. In fact, after obtaining a significant multivariate test for a particular main effect or interaction, customarily one would examine the univariate F tests (see also F Distribution) for each variable to interpret the respective effect. In other words, one would identify the specific dependent variables that contributed to the significant overall effect.
Repeated Measures Designs
If we were to measure math and physics skills at the beginning of the semester and the end of the semester, we would have a multivariate repeated measure. Again, the logic of significance testing in such designs is simply an extension of the univariate case. Note that MANOVA methods are also commonly used to test the significance of univariate repeated measures factors with more than two levels; this application will be discussed later in this section.
Sum Scores versus MANOVA
Even experienced users of ANOVA and MANOVA techniques are often puzzled by the differences in results that sometimes occur when performing a MANOVA on, for example, three variables as compared to a univariate ANOVA on the sum of the three variables. The logic underlying the summing of variables is that each variable contains some "true" value of the variable in question, as well as some random measurement error. Therefore, by summing up variables, the measurement error will sum to approximately 0 across all measurements, and the sum score will become more and more reliable (increasingly equal to the sum of true scores). In fact, under these circumstances, ANOVA on sums is appropriate and represents a very sensitive (powerful) method. However, if the dependent variable is truly multi- dimensional in nature, then summing is inappropriate. For example, suppose that my dependent measure consists of four indicators of success in society, and each indicator represents a completely independent way in which a person could "make it" in life (e.g., successful professional, successful entrepreneur, successful homemaker, etc.). Now, summing up the scores on those variables would be like adding apples to oranges, and the resulting sum score will not be a reliable indicator of a single underlying dimension. Thus, one should treat such data as multivariate indicators of success in a MANOVA.
| To index |
See also Methods for Analysis of Variance, Variance Components and Mixed Model ANOVA/ANCOVA, and Experimental Design (DOE).
Why Compare Individual Sets of Means?
Usually, experimental hypotheses are stated in terms that are more specific than simply main effects or interactions. We may have the specific hypothesis that a particular textbook will improve math skills in males, but not in females, while another book would be about equally effective for both genders, but less effective overall for males. Now generally, we are predicting an interaction here: the effectiveness of the book is modified (qualified) by the student's gender. However, we have a particular prediction concerning the nature of the interaction: we expect a significant difference between genders for one book, but not the other. This type of specific prediction is usually tested via contrast analysis.
Contrast Analysis
Briefly, contrast analysis allows us to test the statistical significance of predicted specific differences in particular parts of our complex design. It is a major and indispensable component of the analysis of every complex ANOVA design.
Post hoc Comparisons
Sometimes we find effects in our experiment that were not expected. Even though in most cases a creative experimenter will be able to explain almost any pattern of means, it would not be appropriate to analyze and evaluate that pattern as if one had predicted it all along. The problem here is one of capitalizing on chance when performing multiple tests post hoc, that is, without a priori hypotheses. To illustrate this point, let us consider the following "experiment." Imagine we were to write down a number between 1 and 10 on 100 pieces of paper. We then put all of those pieces into a hat and draw 20 samples (of pieces of paper) of 5 observations each, and compute the means (from the numbers written on the pieces of paper) for each group. How likely do you think it is that we will find two sample means that are significantly different from each other? It is very likely! Selecting the extreme means obtained from 20 samples is very different from taking only 2 samples from the hat in the first place, which is what the test via the contrast analysis implies. Without going into further detail, there are several so-called post hoc tests that are explicitly based on the first scenario (taking the extremes from 20 samples), that is, they are based on the assumption that we have chosen for our comparison the most extreme (different) means out of k total means in the design. Those tests apply "corrections" that are designed to offset the advantage of post hoc selection of the most extreme comparisons.
| To index |
See also Methods for Analysis of Variance, Variance Components and Mixed Model ANOVA/ANCOVA, and Experimental Design (DOE).
Deviation from Normal Distribution
Assumptions. It is assumed that the dependent variable is measured on at least an interval scale level (see Elementary Concepts). Moreover, the dependent variable should be normally distributed within groups.
Effects of violations. Overall, the F test (see also F Distribution) is remarkably robust to deviations from normality (see Lindman, 1974, for a summary). If the kurtosis (see Basic Statistics and Tables) is greater than 0, then the F tends to be too small and we cannot reject the null hypothesis even though it is incorrect. The opposite is the case when the kurtosis is less than 0. The skewness of the distribution usually does not have a sizable effect on the F statistic. If the n per cell is fairly large, then deviations from normality do not matter much at all because of the central limit theorem, according to which the sampling distribution of the mean approximates the normal distribution, regardless of the distribution of the variable in the population. A detailed discussion of the robustness of the F statistic can be found in Box and Anderson (1955), or Lindman (1974).
Homogeneity of Variances
Assumptions. It is assumed that the variances in the different groups of the design are identical; this assumption is called the homogeneity of variances assumption. Remember that at the beginning of this section we computed the error variance (SS error) by adding up the sums of squares within each group. If the variances in the two groups are different from each other, then adding the two together is not appropriate, and will not yield an estimate of the common within-group variance (since no common variance exists).
Effects of violations. Lindman (1974, p. 33) shows that the F statistic is quite robust against violations of this assumption (heterogeneity of variances; see also Box, 1954a, 1954b; Hsu, 1938).
Special case: correlated means and variances. However, one instance when the F statistic is very misleading is when the means are correlated with variances across cells of the design. A scatterplot of variances or standard deviations against the means will detect such correlations. The reason why this is a "dangerous" violation is the following: Imagine that you have 8 cells in the design, 7 with about equal means but one with a much higher mean. The F statistic may suggest to you a statistically significant effect. However, suppose that there also is a much larger variance in the cell with the highest mean, that is, the means and the variances are correlated across cells (the higher the mean the larger the variance). In that case, the high mean in the one cell is actually quite unreliable, as is indicated by the large variance. However, because the overall F statistic is based on a pooled within-cell variance estimate, the high mean is identified as significantly different from the others, when in fact it is not at all significantly different if one based the test on the within-cell variance in that cell alone.
This pattern -- a high mean and a large variance in one cell -- frequently occurs when there are outliers present in the data. One or two extreme cases in a cell with only 10 cases can greatly bias the mean, and will dramatically increase the variance.
Homogeneity of Variances and Covariances
Assumptions. In multivariate designs, with multiple dependent measures, the homogeneity of variances assumption described earlier also applies. However, since there are multiple dependent variables, it is also required that their intercorrelations (covariances) are homogeneous across the cells of the design. There are various specific tests of this assumption.
Effects of violations. The multivariate equivalent of the F test is Wilks' lambda. Not much is known about the robustness of Wilks' lambda to violations of this assumption. However, because the interpretation of MANOVA results usually rests on the interpretation of significant univariate effects (after the overall test is significant), the above discussion concerning univariate ANOVA basically applies, and important significant univariate effects should be carefully scrutinized.
Special case: ANCOVA. A special serious violation of the homogeneity of variances/covariances assumption may occur when covariates are involved in the design. Specifically, if the correlations of the covariates with the dependent measure(s) are very different in different cells of the design, gross misinterpretations of results may occur. Remember that in ANCOVA, we in essence perform a regression analysis within each cell to partition out the variance component due to the covariates. The homogeneity of variances/covariances assumption implies that we perform this regression analysis subject to the constraint that all regression equations (slopes) across the cells of the design are the same. If this is not the case, serious biases may occur. There are specific tests of this assumption, and it is advisable to look at those tests to ensure that the regression equations in different cells are approximately the same.
Sphericity and Compound Symmetry
Reasons for Using the Multivariate Approach to Repeated Measures ANOVA. In repeated measures ANOVA containing repeated measures factors with more than two levels, additional special assumptions enter the picture: The compound symmetry assumption and the assumption of sphericity. Because these assumptions rarely hold (see below), the MANOVA approach to repeated measures ANOVA has gained popularity in recent years (both tests are automatically computed in ANOVA/MANOVA). The compound symmetry assumption requires that the variances (pooled within-group) and covariances (across subjects) of the different repeated measures are homogeneous (identical). This is a sufficient condition for the univariate F test for repeated measures to be valid (i.e., for the reported F values to actually follow the F distribution). However, it is not a necessary condition. The sphericity assumption is a necessary and sufficient condition for the F test to be valid; it states that the within-subject "model" consists of independent (orthogonal) components. The nature of these assumptions, and the effects of violations are usually not well-described in ANOVA textbooks; in the following paragraphs we will try to clarify this matter and explain what it means when the results of the univariate approach differ from the multivariate approach to repeated measures ANOVA.
The necessity of independent hypotheses. One general way of looking at ANOVA is to consider it a model fitting procedure. In a sense we bring to our data a set of a priori hypotheses; we then partition the variance (test main effects, interactions) to test those hypotheses. Computationally, this approach translates into generating a set of contrasts (comparisons between means in the design) that specify the main effect and interaction hypotheses. However, if these contrasts are not independent of each other, then the partitioning of variances runs afoul. For example, if two contrasts A and B are identical to each other and we partition out their components from the total variance, then we take the same thing out twice. Intuitively, specifying the two (not independent) hypotheses "the mean in Cell 1 is higher than the mean in Cell 2" and "the mean in Cell 1 is higher than the mean in Cell 2" is silly and simply makes no sense. Thus, hypotheses must be independent of each other, or orthogonal (the term orthogonality was first used by Yates, 1933).
Independent hypotheses in repeated measures. The general algorithm implemented will attempt to generate, for each effect, a set of independent (orthogonal) contrasts. In repeated measures ANOVA, these contrasts specify a set of hypotheses about differences between the levels of the repeated measures factor. However, if these differences are correlated across subjects, then the resulting contrasts are no longer independent. For example, in a study where we measured learning at three times during the experimental session, it may happen that the changes from time 1 to time 2 are negatively correlated with the changes from time 2 to time 3: subjects who learn most of the material between time 1 and time 2 improve less from time 2 to time 3. In fact, in most instances where a repeated measures ANOVA is used, one would probably suspect that the changes across levels are correlated across subjects. However, when this happens, the compound symmetry and sphericity assumptions have been violated, and independent contrasts cannot be computed.
Effects of violations and remedies. When the compound symmetry or sphericity assumptions have been violated, the univariate ANOVA table will give erroneous results. Before multivariate procedures were well understood, various approximations were introduced to compensate for the violations (e.g., Greenhouse & Geisser, 1959; Huynh & Feldt, 1970), and these techniques are still widely used.
MANOVA approach to repeated measures. To summarize, the problem of compound symmetry and sphericity pertains to the fact that multiple contrasts involved in testing repeated measures effects (with more than two levels) are not independent of each other. However, they do not need to be independent of each other if we use multivariate criteria to simultaneously test the statistical significance of the two or more repeated measures contrasts. This "insight" is the reason why MANOVA methods are increasingly applied to test the significance of univariate repeated measures factors with more than two levels. We wholeheartedly endorse this approach because it simply bypasses the assumption of compound symmetry and sphericity altogether.
Cases when the MANOVA approach cannot be used. There are instances (designs) when the MANOVA approach cannot be applied; specifically, when there are few subjects in the design and many levels on the repeated measures factor, there may not be enough degrees of freedom to perform the multivariate analysis. For example, if we have 12 subjects and p = 4 repeated measures factors, each at k = 3 levels, then the four-way interaction would "consume" (k-1)p = 24 = 16 degrees of freedom. However, we have only 12 subjects, so in this instance the multivariate test cannot be performed.
Differences in univariate and multivariate results. Anyone whose research involves extensive repeated measures designs has seen cases when the univariate approach to repeated measures ANOVA gives clearly different results from the multivariate approach. To repeat the point, this means that the differences between the levels of the respective repeated measures factors are in some way correlated across subjects. Sometimes, this insight by itself is of considerable interest.
| To index |
Several chapters in this textbook discuss methods for performing analysis of variance. Although many of the available statistics overlap in the different chapters, each is best suited for particular applications.
General ANCOVA/MANCOVA: This chapter includes discussions of full factorial designs, repeated measures designs, mutivariate design (MANOVA), designs with balanced nesting (designs can be unbalanced, i.e., have unequal n), for evaluating planned and post-hoc comparisons, etc.
General Linear Models: This extremely comprehensive chapter discusses a complete implementation of the general linear model, and describes the sigma-restricted as well as the overparameterized approach. This chapter includes information on incomplete designs, complex analysis of covariance designs, nested designs (balanced or unbalanced), mixed model ANOVA designs (with random effects), and huge balanced ANOVA designs (efficiently). It also contains descriptions of six types of Sums of Squares.
General Stepwise Regression: This chapter discusses the between subject designs and multivariate designs which are appropriate for stepwise regression as well as discussing how to perform stepwise and best-subset model building (for continuous as well as categorical predictors).
Mixed ANCOVA and Variance Components: This chapter includes discussions of experiments with random effects (mixed model ANOVA), estimating variance components for random effects, or large main effect designs (e.g., with factors with over 100 levels) with or without random effects, or large designs with many factors, when you do not need to estimate all interactions.
Experimental Design (DOE): This chapter includes discussions of standard experimental designs for industrial/manufacturing applications, including 2**(k-p) and 3**(k-p) designs, central composite and non-factorial designs, designs for mixtures, D and A optimal designs, and designs for arbitrarily constrained experimental regions.
Repeatability and Reproducibility Analysis (in the Process Analysis chapter): This section in the Process Analysis chapter includes a discussion of specialized designs for evaluating the reliability and precision of measurement systems; these designs usually include two or three random factors, and specialized statistics can be computed for evaluating the quality of a measurement system (typically in industrial/manufacturing applications).
Breakdown Tables (in the Basic Statistics chapter): This chapter includes discussions of experiments with only one factor (and many levels), or with multiple factors, when a complete ANOVA table is not required.
| To index |