Uniform Distribution. The discrete Uniform distribution (the term first used by Uspensky, 1937) has density function:

f(x) = 1/N          x = 1, 2, ..., N

The continuous Uniform distribution has density function: where

f(x) = 1/(b-a)        a < x < b

a     is the lower limit of the interval from which points will be selected
b     is the upper limit of the interval from which points will be selected

Unimodal Distribution. A distribution that has only one mode. A typical example is the normal distribution which happens to be also symmetrical but many unimodal distributions are not symmetrical (e.g., typically the distribution of income is not symmetrical but "left-skewed"; see skewness). See also bimodal distribution, multimodal distribution.

Unit Penalty. In several search algorithms, a penalty factor which is multiplied by the number of units in the network and added to the error of the network, when comparing the performance of the network with others. This has the effect of selecting smaller networks at the expense of larger ones. See also, Penalty Function.

Unsupervised Learning in Neural Networks. Training algorithms which adjust the weights in a neural network by reference to a training data set including input variables only. Unsupervised learning algorithms attempt to locate clusters in the input data.

See also, Kohonen algorithm.

Unwieghted Means. If the cell frequencies in a multi-factor ANOVA design are unequal, then the unweighted means (for levels of a factor) are calculated from the means of sub-groups without weighting, that is, without adjusting for the differences between the sub-group frequencies.

Variance. The variance (this term was first used by Fisher, 1918a) of a population of values is computed as:

² = (x_i-µ)²/N

where
µ    is the population mean
N   is the population size.
The unbiased sample estimate of the population variance is computed as:

s² = (x_i-xbar)²/n-1

where
xbar   is the sample mean
n        is the sample size.

See also, Descriptive Statistics.

Variance Components (in Mixed Model ANOVA) The term variance components is used in the context of experimental designs with random effects, to denote the estimate of the (amount of) variance that can be attributed to those effects. For example, if one were interested in the effect that the quality of different schools has on academic proficiency, one could select a sample of schools to estimate the amount of variance in academic proficiency (component of variance) that is attributable to differences between schools.

See also, Analysis of Variance and Variance Components and Mixed Model ANOVA/ANCOVA.

Variance Inflation Factor (VIF). The diagonal elements of the inverse correlation matrix (i.e., -1 times the diagonal elements of the sweep matrix) for variables that are in the equation are also sometimes called variance inflation factors (VIF; e.g., see Neter, Wasserman, Kutner, 1985). This terminology denotes the fact that the variances of the standardized regression coefficients can be computed as the product of the residual variance (for the correlation transformed model) times the respective diagonal elements of the inverse correlation matrix. If the predictor variables are uncorrelated, then the diagonal elements of the inverse correlation matrix are equal to 1.0; thus, for correlated predictors, these elements represent an "inflation factor" for the variance of the regression coefficients, due to the redundancy of the predictors.

See also, Multiple Regression.

Voronoi. The Voronoi tessellation graph plots values of two variables X and Y in a scatterplot, then divides the space between individual data points into regions such that the boundaries surrounding each data point enclose an area that is closer to that data point than to any other neighboring points.

Voronoi Scatterplot. This specialized univariate scatterplot is more an analytic technique than just a method to graphically present data. The solutions it offers, help to model a variety of phenomena in natural and social sciences (e.g., Coombs, 1964; Ripley, 1981). The program divides the space between the individual data points represented by XY coordinates in 2D space. The division is such that each of the data points is surrounded by boundaries including only the area that is closer to its respective "center" data point than to any other data point.

The particular ways in which this method is used depends largely on specific research areas, however, in many of them, it is helpful to add additional dimensions to this plot by using categorization options (as shown in the example below).

See also, Data Reduction.

Wald Statistic. The results Scrollsheet with the parameter estimates for the Cox proportional hazard regression model includes the so-called Wald statistic, and the p level for that statistic. This statistic is a test of significance of the regression coefficient; it is based on the asymptotic normality property of maximum likelihood estimates, and is computed as:

W = * 1/Var() *

In this formula, stands for the parameter estimates, and Var() stands for the asymptotic variance of the parameter estimates. The Wald statistic is tested against the Chi-square distribution.

Weibull Distribution. The Weibull distribution (Weibull, 1939, 1951; see also Lieblein, 1955) has density function (for positive parameters b, c, and ):

f(x) = c/b*[(x-)/b]^c-1 * e^{-[(x-)/b]^c}
< x,  b > 0,  c > 0

where
b     is the scale parameter of the distribution
c     is the shape parameter of the distribution
   is the location parameter of the distribution
e     is the base of the natural logarithm, sometimes called Euler's e (2.71...)

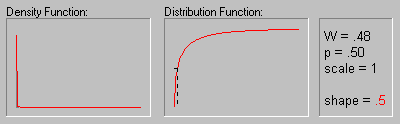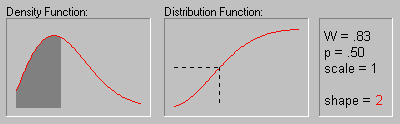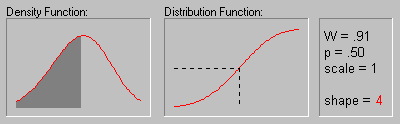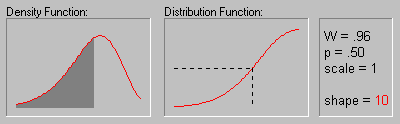
The animation above shows the Weibull distribution as the shape parameter increases (.5, 1, 2, 3, 4, 5, and 10).

Weigend Regularization. A modification to the error function used in iterative training algorithms, so that large weight values are penalized, allowing a network to automatically determine its own level of complexity and so avoid overlearning (Weigend et. al., 1991). See, Neural Networks.

Weighted Least Squares (in Regression). In some cases it is desirable to apply differential weights to the observations in a regression analysis, and to compute so-called weighted least squares regression estimates. This method is commonly applied when the variances of the residuals are not constant over the range of the independent variable values. In that case, one can apply the inverse values of the variances for the residuals as weights and compute weighted least squares estimates. (In practice, these variances are usually not known, however, they are often proportional to the values of the independent variable(s), and this proportionality can be exploited to compute appropriate case weights.) Neter, Wasserman, and Kutner (1985) describe an example of such an analysis.

Win Frequencies in Neural Networks. In a Kohonen network, the number of times that each radial unit is the winner when the data set is executed. Units which win frequently represent cluster centers in the topological map. See, Neural Networks.

Wire. A wire is a line, usually curved, used in a path diagram to represent variances and covariances of exogenous variables.