• Data Mining
• Data Warehousing
• On-Line Analytic Processing (OLAP)
• Exploratory Data Analysis (EDA) and Data Mining Techniques
  • EDA vs. Hypothesis Testing
  • Computational EDA Techniques
  • Graphical (data visualization) EDA techniques
  • Verification of results of EDA
• Neural Networks

Data Mining

StatSoft defines Data Mining as an analytic process designed to explore large amounts of (typically business or market related) data in search for consistent patterns and/or systematic relationships between variables, and then to validate the findings by applying the detected patterns to new subsets of data. The process thus consists of three basic stages: exploration, model building or pattern definition, and validation/verification. Ideally, if the nature of available data allows, it is typically repeated iteratively until a "robust" model is identified. However, in business practice the options to validate the model at the stage of analysis are typically limited and, thus, the initial results often have the status of heuristics that could influence the decision process (e.g., "The data appear to indicate that the probability of trying sleeping pills increases with age faster in females than in males.").

The concept of Data Mining is becoming increasingly popular as a business information management tool where it is expected to reveal knowledge structures that can guide decisions in conditions of limited certainty. Recently, there has been increased interest in developing new analytic techniques specifically designed to address the issues relevant to business Data Mining (e.g., Classification Trees), but Data Mining is still based on the conceptual principles of traditional Exploratory Data Analysis (EDA) and modeling and it shares with them both general approaches and specific techniques.

However, an important general difference in the focus and purpose between Data Mining and the traditional Exploratory Data Analysis (EDA) is that Data Mining is more oriented towards applications than the basic nature of the underlying phenomena. In other words, Data Mining is relatively less concerned with identifying the specific relations between the involved variables. For example, uncovering the nature of the underlying functions or the specific types of interactive, multivariate dependencies between variables are not the main goal of Data Mining. Instead, the focus is on producing a solution that can generate useful predictions. Therefore, Data Mining accepts among others a "black box" approach to data exploration or knowledge discovery and uses not only the traditional Exploratory Data Analysis (EDA) techniques, but also such techniques as Neural Networks which can generate valid predictions but are not capable of identifying the specific nature of the interrelations between the variables on which the predictions are based.

Data Mining is often considered to be "a blend of statistics, AI [artificial intelligence], and data base research" (Pregibon, 1997, p. 8), which until very recently was not commonly recognized as a field of interest for statisticians, and was even considered by some "a dirty word in Statistics" (Pregibon, 1997, p. 8). Due to its applied importance, however, the field emerges as a rapidly growing and major area (also in statistics) where important theoretical advances are being made (see, for example, the recent annual International Conferences on Knowledge Discovery and Data Mining, co-hosted in 1997 by the American Statistical Association).

For information on Data Mining techniques, see Exploratory Data Analysis (EDA) and Data Mining Techniques, see also Neural Networks; for a comprehensive overview and discussion of Data Mining, see Fayyad, Piatetsky-Shapiro, Smyth, and Uthurusamy (1996). Representative selections of articles on Data Mining can be found in Proceedings from the American Association of Artificial Intelligence Workshops on Knowledge Discovery in Databases published by AAAI Press (e.g., Piatetsky-Shapiro, 1993; Fayyad & Uthurusamy, 1994).

Data mining is often treated as the natural extension of the data warehousing concept (see below).

To index

Data Warehousing

StatSoft defines data warehousing as a process of organizing the storage of large, multivariate data sets in a way that facilitates the retrieval of information for analytic purposes.

The most efficient data warehousing architecture will be capable of incorporating or at least referencing all data available in the relevant enterprise-wide information management systems, using designated technology suitable for corporate data base management (e.g., Oracle, Sybase, MS SQL Server; also, high-performance data warehousing technology allowing the users to organize and efficiently reference for analytic purposes enterprise repositories of data of practically any complexity is offered in StatSoft enterprise systems such as SENS [STATISTICA Enterprise System] and SEWSS [STATISTICA Enterprise-Wide SPC System]).

To index

On-Line Analytic Processing (OLAP)

The term On-Line Analytic Processing - OLAP (or Fast Analysis of Shared Multidimensional Information - FASMI) refers to technology that allows users of multidimensional data bases to generate on-line descriptive or comparative summaries ("views") of data and other analytic queries. Note that despite its name, analyses referred to as OLAP do not need to be performed truly "on-line" (or in real-time); the term applies to analyses of multidimensional data bases (that may, obviously, contain dynamically updated information) through efficient "multidimensional" queries that reference various types of data. OLAP facilities can be integrated into corporate (enterprise-wide) data base systems and they allow analysts and managers to monitor the performance of the business (e.g., such as various aspects of the manufacturing process or numbers and types of completed transactions at different locations) or the market. The final result of OLAP techniques can be very simple (e.g., frequency tables, descriptive statistics, simple cross-tabulations) or more complex (e.g., they may involve seasonal adjustments, removal of outliers, and other forms of cleaning the data). Although Data Mining techniques can operate on any kind of unprocessed or even unstructured information, they can also be applied to the data views and summaries generated by OLAP to provide more in-depth and often more multidimensional knowledge. In this sense, Data Mining techniques could be considered to represent either a different analytic approach (serving different purposes than OLAP) or as an analytic extension of OLAP.

To index

Exploratory Data Analysis (EDA)

EDA vs. Hypothesis Testing

As opposed to traditional hypothesis testing designed to verify a priori hypotheses about relations between variables (e.g., "There is a positive correlation between the AGE of a person and his/her RISK TAKING disposition"), exploratory data analysis (EDA) is used to identify systematic relations between variables when there are no (or not complete) a priori expectations as to the nature of those relations. In a typical exploratory data analysis process, many variables are taken into account and compared, using a variety of techniques in the search for systematic patterns.

Computational EDA techniques

Computational exploratory data analysis methods include both simple basic statistics and more advanced, designated multivariate exploratory techniques designed to identify patterns in multivariate data sets.

Basic statistical exploratory methods. The basic statistical exploratory methods include such techniques as examining distributions of variables (e.g., to identify highly skewed or non-normal, such as bi-modal patterns), reviewing large correlation matrices for coefficients that meet certain thresholds (see example above), or examining multi-way frequency tables (e.g., "slice by slice" systematically reviewing combinations of levels of control variables).

Multivariate exploratory techniques. Multivariate exploratory techniques designed specifically to identify patterns in multivariate (or univariate, such as sequences of measurements) data sets include: Cluster Analysis, Factor Analysis, Discriminant Function Analysis, Multidimensional Scaling, Log-linear Analysis, Canonical Correlation, Stepwise Linear and Nonlinear (e.g., Logit) Regression, Correspondence Analysis, Time Series Analysis, and Classification Trees.

Neural Networks. Neural Networks are analytic techniques modeled after the (hypothesized) processes of learning in the cognitive system and the neurological functions of the brain and capable of predicting new observations (on specific variables) from other observations (on the same or other variables) after executing a process of so-called learning from existing data.

For more information, see Neural Networks; see also STATISTICA Neural Networks.

Graphical (data visualization) EDA techniques

A large selection of powerful exploratory data analytic techniques is also offered by graphical data visualization methods that can identify relations, trends, and biases "hidden" in unstructured data sets.

Brushing. Perhaps the most common and historically first widely used technique explicitly identified as graphical exploratory data analysis is brushing, an interactive method allowing one to select on-screen specific data points or subsets of data and identify their (e.g., common) characteristics, or to examine their effects on relations between relevant variables. Those relations between variables can be visualized by fitted functions (e.g., 2D lines or 3D surfaces) and their confidence intervals, thus, for example, one can examine changes in those functions by interactively (temporarily) removing or adding specific subsets of data. For example, one of many applications of the brushing technique is to select (i.e., highlight) in a matrix scatterplot all data points that belong to a certain category (e.g., a "medium" income level, see the highlighted subset in the fourth component graph of the first row in the illustration below):

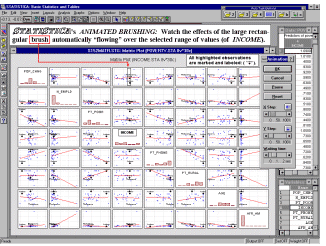
in order to examine how those specific observations contribute to relations between other variables in the same data set (e.g, the correlation between the "debt" and "assets" in the current example). If the brushing facility supports features like "animated brushing" or "automatic function re-fitting", one can define a dynamic brush that would move over the consecutive ranges of a criterion variable (e.g., "income" measured on a continuous scale or a discrete [3-level] scale as on the illustration above) and examine the dynamics of the contribution of the criterion variable to the relations between other relevant variables in the same data set.

Other graphical EDA techniques. Other graphical exploratory analytic techniques include function fitting and plotting, data smoothing, overlaying and merging of multiple displays, categorizing data, splitting/merging subsets of data in graphs, aggregating data in graphs, identifying and marking subsets of data that meet specific conditions, icon plots,

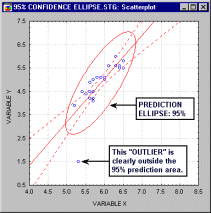
shading, plotting confidence intervals and confidence areas (e.g., ellipses),

generating tessellations, spectral planes,

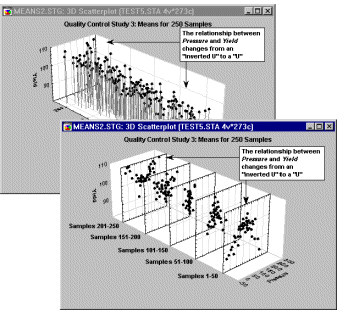
integrated layered compressions,

and projected contours, data image reduction techniques, interactive (and continuous) rotation

with animated stratification (cross-sections) of 3D displays, and selective highlighting of specific series and blocks of data.

Verification of results of EDA

The exploration of data can only serve as the first stage of data analysis and its results can be treated as tentative at best as long as they are not confirmed, e.g., crossvalidated, using a different data set (or and independent subset). If the result of the exploratory stage suggests a particular model, then its validity can be verified by applying it to a new data set and testing its fit (e.g., testing its predictive validity). Case selection conditions can be used to quickly define subsets of data (e.g., for estimation and verification), and for testing the robustness of results.

To index

Neural Networks

Neural Networks are analytic techniques modeled after the (hypothesized) processes of learning in the cognitive system and the neurological functions of the brain and capable of predicting new observations (on specific variables) from other observations (on the same or other variables) after executing a process of so-called learning from existing data. Neural Networks is one of the Data Mining techniques.

The first step is to design a specific network architecture (that includes a specific number of "layers" each consisting of a certain number of "neurons"). The size and structure of the network needs to match the nature (e.g., the formal complexity) of the investigated phenomenon. Because the latter is obviously not known very well at this early stage, this task is not easy and often involves multiple "trials and errors." (Now, there is, however, neural network software that applies artificial intelligence techniques to aid in that tedious task and finds "the best" network architecture.)

The new network is then subjected to the process of "training." In that phase, neurons apply an iterative process to the number of inputs (variables) to adjust the weights of the network in order to optimally predict (in traditional terms one could say, find a "fit" to) the sample data on which the "training" is performed. After the phase of learning from an existing data set, the new network is ready and it can then be used to generate predictions.

The resulting "network" developed in the process of "learning" represents a pattern detected in the data. Thus, in this approach, the "network" is the functional equivalent of a model of relations between variables in the traditional model building approach. However, unlike in the traditional models, in the "network," those relations cannot be articulated in the usual terms used in statistics or methodology to describe relations between variables (such as, for example, "A is positively correlated with B but only for observations where the value of C is low and D is high"). Some neural networks can produce highly accurate predictions; they represent, however, a typical a-theoretical (one can say, "a black box") research approach. That approach is concerned only with practical considerations, that is, with the predictive validity of the solution and its applied relevance and not with the nature of the underlying mechanism or its relevance for any "theory" of the underlying phenomena.

However, it should be mentioned that Neural Network techniques can also be used as a component of analyses designed to build explanatory models because Neural Networks can help explore data sets in search for relevant variables or groups of variables; the results of such explorations can then facilitate the process of model building. Moreover, now there is neural network software that uses sophisticated algorithms to search for the most relevant input variables, thus potentially contributing directly to the model building process.

One of the major advantages of neural networks is that, theoretically, they are capable of approximating any continuous function, and thus the researcher does not need to have any hypotheses about the underlying model, or even to some extent, which variables matter. An important disadvantage, however, is that the final solution depends on the initial conditions of the network, and, as stated before, it is virtually impossible to "interpret" the solution in traditional, analytic terms, such as those used to build theories that explain phenomena.

Some authors stress the fact that neural networks use, or one should say, are expected to use, massively parallel computation models. For example Haykin (1994) defines neural network as:

"a massively parallel distributed processor that has a natural propensity for storing experiential knowledge and making it available for use. It resembles the brain in two respects: (1) Knowledge is acquired by the network through a learning process, and (2) Interneuron connection strengths known as synaptic weights are used to store the knowledge." (p. 2).

However, as Ripley (1996) points out, the vast majority of contemporary neural network applications run on single-processor computers and he argues that a large speed-up can be achieved not only by developing software that will take advantage of multiprocessor hardware by also by designing better (more efficient) learning algorithms.

Neural networks is one of the methods used in Data Mining; see also Exploratory Data Analysis. For more information on neural networks, see Haykin (1994), Masters (1995), Ripley (1996), and Welstead (1994). For a discussion of neural networks as statistical tools, see Warner and Misra (1996). See also, STATISTICA Neural Networks.

To index