Basic Ideas
Classification trees are used to predict membership of cases or objects in the classes of a categorical dependent variable from their measurements on one or more predictor variables. Classification tree analysis is one of the main techniques used in so-called Data Mining.
The goal of classification trees is to predict or explain responses on a categorical dependent variable, and as such, the available techniques have much in common with the techniques used in the more traditional methods of Discriminant Analysis, Cluster Analysis, Nonparametric Statistics, and Nonlinear Estimation. The flexibility of classification trees make them a very attractive analysis option, but this is not to say that their use is recommended to the exclusion of more traditional methods. Indeed, when the typically more stringent theoretical and distributional assumptions of more traditional methods are met, the traditional methods may be preferable. But as an exploratory technique, or as a technique of last resort when traditional methods fail, classification trees are, in the opinion of many researchers, unsurpassed.
What are classification trees? Imagine that you want to devise a system for sorting a collection of coins into different classes (perhaps pennies, nickels, dimes, quarters). Suppose that there is a measurement on which the coins differ, say diameter, which can be used to devise a hierarchical system for sorting coins. You might roll the coins on edge down a narrow track in which a slot the diameter of a dime is cut. If the coin falls through the slot it is classified as a dime, otherwise it continues down the track to where a slot the diameter of a penny is cut. If the coin falls through the slot it is classified as a penny, otherwise it continues down the track to where a slot the diameter of a nickel is cut, and so on. You have just constructed a classification tree. The decision process used by your classification tree provides an efficient method for sorting a pile of coins, and more generally, can be applied to a wide variety of classification problems.
The study and use of classification trees are not widespread in the fields of probability and statistical pattern recognition (Ripley, 1996), but classification trees are widely used in applied fields as diverse as medicine (diagnosis), computer science (data structures), botany (classification), and psychology (decision theory). Classification trees readily lend themselves to being displayed graphically, helping to make them easier to interpret than they would be if only a strict numerical interpretation were possible.

Classification trees can be and sometimes are quite complex. However, graphical procedures can be developed to help simplify interpretation even for complex trees. If one's interest is mainly in the conditions that produce a particular class of response, perhaps a High response, a 3D Contour Plot can be produced to identify which terminal node of the classification tree classifies most of the cases with High responses.
In the example illustrated by this 3D Contour Plot, one could "follow the branches" leading to terminal node 8 to obtain an understanding of the conditions leading to High responses.
Amenability to graphical display and ease of interpretation are perhaps partly responsible for the popularity of classification trees in applied fields, but two features that characterize classification trees more generally are their hierarchical nature and their flexibility.
For information on techniques and issues in computing classification trees, see Computational Methods. See also Exploratory Data Analysis and Data Mining Techniques.
| To index |
Characteristics of Classification Trees
Hierarchical Nature of Classification Trees
Breiman et al. (1984) give a number of examples of the use of classification trees. As one example, when heart attack patients are admitted to a hospital, dozens of tests are often performed to obtain physiological measures such as heart rate, blood pressure, and so on. A wide variety of other information is also obtained, such as the patient's age and medical history. Patients subsequently can be tracked to see if they survive the heart attack, say, at least 30 days. It would be useful in developing treatments for heart attack patients, and in advancing medical theory on heart failure, if measurements taken soon after hospital admission could be used to identify high-risk patients (those who are not likely to survive at least 30 days). One classification tree that Breiman et al. (1984) developed to address this problem was a simple, three question decision tree. Verbally, the binary classification tree can be described by the statement, "If the patient's minimum systolic blood pressure over the initial 24 hour period is greater than 91, then if the patient's age is over 62.5 years, then if the patient displays sinus tachycardia, then and only then the patient is predicted not to survive for at least 30 days." It is easy to conjure up the image of a decision "tree" from such a statement. A hierarchy of questions are asked and the final decision that is made depends on the answers to all the previous questions. Similarly, the relationship of a leaf to the tree on which it grows can be described by the hierarchy of splits of branches (starting from the trunk) leading to the last branch from which the leaf hangs. The hierarchical nature of classification trees is one of their most basic features (but the analogy with trees in nature should not be taken too far; most decision trees are drawn downward on paper, so the more exact analogy in nature would be a decision root system leading to the root tips, hardly a poetic image).
The hierarchical nature of classification trees is illustrated by a comparison to the decision-making procedure employed in Discriminant Analysis. A traditional linear discriminant analysis of the heart attack data would produce a set of coefficients defining the single linear combination of blood pressure, patient age, and sinus tachycardia measurements that best differentiates low risk from high risk patients. A score for each patient on the linear discriminant function would be computed as a composite of each patient's measurements on the three predictor variables, weighted by the respective discriminant function coefficients. The predicted classification of each patient as a low risk or a high risk patient would be made by simultaneously considering the patient's scores on the three predictor variables. That is, suppose P (minimum systolic blood Pressure over the 24 hour period), A (Age in years), and T (presence of sinus Tachycardia: 0 = not present; 1 = present) are the predictor variables, p, a, and t, are the corresponding linear discriminant function coefficients, and c is the "cut point" on the discriminant function for separating the two classes of heart attack patients. The decision equation for each patient would be of the form, "if pP + aA + tT - c is less than or equal to zero, the patient is low risk, else the patient is in high risk."
In comparison, the decision tree developed by Breiman et al. (1984) would have the following hierarchical form, where p, a, and t would be -91, -62.5, and 0, respectively, "If p + P is less than or equal to zero, the patient is low risk, else if a + A is less than or equal to zero, the patient is low risk, else if t + T is less than or equal to zero, the patient is low risk, else the patient is high risk." Superficially, the Discriminant Analysis and classification tree decision processes might appear similar, because both involve coefficients and decision equations. But the difference of the simultaneous decisions of Discriminant Analysis from the hierarchical decisions of classification trees cannot be emphasized enough.
The distinction between the two approaches can perhaps be made most clear by considering how each analysis would be performed in Regression. Because risk in the example of Breiman et al. (1984) is a dichotomous dependent variable, the Discriminant Analysis predictions could be reproduced by a simultaneous multiple regression of risk on the three predictor variables for all patients. The classification tree predictions could only be reproduced by three separate simple regression analyses, where risk is first regressed on P for all patients, then risk is regressed on A for patients not classified as low risk in the first regression, and finally, risk is regressed on T for patients not classified as low risk in the second regression. This clearly illustrates the simultaneous nature of Discriminant Analysis decisions as compared to the recursive, hierarchical nature of classification trees decisions, a characteristic of classification trees that has far-reaching implications.
Flexibility of Classification Trees
Another distinctive characteristic of classification trees is their flexibility. The ability of classification trees to examine the effects of the predictor variables one at a time, rather than just all at once, has already been described, but there are a number of other ways in which classification trees are more flexible than traditional analyses. The ability of classification trees to perform univariate splits, examining the effects of predictors one at a time, has implications for the variety of types of predictors that can be analyzed. In the Breiman et al. (1984) heart attack example, blood pressure and age were continuous predictors, but presence of sinus tachycardia was a categorical (two-level) predictor. Even if sinus tachycardia was measured as a three-level categorical predictor (perhaps coded as 0 = not present; 1 = present; 3 = unknown or unsure), without any underlying continuous dimension represented by the values assigned to its levels, univariate splits on the predictor variables could still be easily performed. Additional decisions would be added to the decision tree to exploit any additional information on risk provided by the additional category. To summarize, classification trees can be computed for categorical predictors, continuous predictors, or any mix of the two types of predictors when univariate splits are used.
Traditional linear discriminant analysis requires that the predictor variables be measured on at least an interval scale. For classification trees based on univariate splits for ordinal scale predictor variables, it is interesting that any monotonic transformation of the predictor variables (i.e., any transformation that preserves the order of values on the variable) will produce splits yielding the same predicted classes for the cases or objects (if the CART-style univariate split selection method is used, see Breimen et al., 1984). Therefore, classification trees based on univariate splits can be computed without concern for whether a unit change on a continuous predictor represents a unit change on the dimension underlying the values on the predictor variable; it need only be assumed that predictors are measured on at least an ordinal scale. In short, assumptions regarding the level of measurement of predictor variables are less stringent.
Classification trees are not limited to univariate splits on the predictor variables. When continuous predictors are indeed measured on at least an interval scale, linear combination splits, similar to the splits for linear discriminant analysis, can be computed for classification trees. However, the linear combination splits computed for Classification Trees do differ in important ways from the linear combination splits computed for Discriminant Analysis. In linear discriminant analysis the number of linear discriminant functions that can be extracted is the lesser of the number of predictor variables or the number of classes on the dependent variable minus one. The recursive approach implemented for Classification Treesmodule does not face this limitation. For example, dozens of recursive, linear combination splits potentially could be performed when there are dozens of predictor variables but only two classes on the dependent variable. This compares with the single linear combination split that could be performed using traditional, non-recursive Iinear discriminant analysis, which could leave a substantial amount of the information in the predictor variables unused.
Now consider the situation in which there are many categories but few predictors. Suppose you were trying to sort coins into classes (perhaps pennies, nickels, dimes, and quarters) based only on thickness and diameter measurements. Using traditional linear discriminant analysis, at most two linear discriminant functions could be extracted, and the coins could be successfully sorted only if there were no more than two dimensions represented by linear combinations of thickness and diameter on which the coins differ. Again, the approach implemented for Classification Trees does not face a limitation on the number of linear combination splits that can be formed.
The approach implemented for Classification Trees for linear combination splits can also be used as the analysis method for constructing classification trees using univariate splits. Actually, a univariate split is just a special case of a linear combination split. Imagine a linear combination split in which the coefficients for creating the weighted composite were zero for all predictor variables except one. Since scores on the weighted composite would depend only on the scores on the one predictor variable with the nonzero coefficient, the resulting split would be a univariate split.
The approach implemented for Classification Trees for the Discriminant-based univariate split selection method for categorical and ordered predictors and for the Discriminant-based linear combination split selection method for ordered predictors is an adaption of the algorithms used in QUEST (Quick, Unbiased, Efficient Statistical Trees). QUEST is a classification tree program developed by Loh and Shih (1997) that employs a modification of recursive quadratic discriminant analysis and includes a number of innovative features for improving the reliability and efficiency of the classification trees that it computes.
The algorithms used in QUEST are fairly technical, but the Classification Trees module also offers a Split selection method option based on a conceptually simpler approach. The CART-style univariate split selection method is an adaption of the algorithms used in CART, as described by Breiman et al. (1984). CART (Classification And Regression Trees) is a classification tree program that uses an exhaustive grid search of all possible univariate splits to find the splits for a classification tree.
The QUEST and CART analysis options compliment each other nicely. CART searches can be lengthy when there are a large number of predictor variables with many levels, and it is biased toward choosing predictor variables with more levels for splits, but because it employs an exhaustive search, it is guaranteed to find the splits producing the best classification (in the learning sample, but not necessarily in cross-validation samples).
QUEST is fast and unbiased. The speed advantage of QUEST over CART is particularly dramatic when the predictor variables have dozens of levels (Loh & Shih, 1997, report an analysis completed by QUEST in 1 CPU second that took CART 30.5 CPU hours to complete). QUEST's lack of bias in variable selection for splits is also a distinct advantage when some predictor variable have few levels and other predictor variables have many levels (predictors with many levels are more likely to produce "fluke theories," which fit the data well but have low predictive accuracy, see Doyle, 1973, and Quinlan & Cameron-Jones, 1995). Finally, QUEST does not sacrifice predictive accuracy for speed (Lim, Loh, & Shih, 1997). Together, the QUEST and CART options allow one to fully exploit the flexibility of classification trees.
The Power and Pitfalls of Classification Trees
The advantages of classification trees over traditional methods such as linear discriminant analysis, at least in some applications, can be illustrated using a simple, fictitious data set. To keep the presentation even-handed, other situations in which linear discriminant analysis would outperform classification trees are illustrated using a second data set.
Suppose you have records of the Longitude and Latitude coordinates at which 37 storms reached hurricane strength for two classifications of hurricanes--Baro hurricanes and Trop hurricanes. The fictitious data shown below were presented for illustrative purposes by Elsner, Lehmiller, and Kimberlain (1996), who investigated the differences between baroclinic and tropical North Atlantic hurricanes.
| DATA: Barotrop.sta 3v | ||
|---|---|---|
| LONGITUD | LATITUDE | CLASS |
| 59.00 59.50 60.00 60.50 61.00 61.00 61.50 61.50 62.00 63.00 63.50 64.00 64.50 65.00 65.00 65.00 65.50 65.50 65.50 66.00 66.00 66.00 66.50 66.50 66.50 67.00 67.50 68.00 68.50 69.00 69.00 69.50 69.50 70.00 70.50 71.00 71.50 |
17.00 21.00 12.00 16.00 13.00 15.00 17.00 19.00 14.00 15.00 19.00 12.00 16.00 12.00 15.00 17.00 16.00 19.00 21.00 13.00 14.00 17.00 17.00 18.00 21.00 14.00 18.00 14.00 18.00 13.00 15.00 17.00 19.00 12.00 16.00 17.00 21.00 |
BARO BARO BARO BARO BARO BARO BARO BARO BARO TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP TROP BARO BARO BARO BARO BARO BARO BARO BARO BARO BARO |
A linear discriminant analysis of hurricane Class (Baro or Trop) using Longitude and Latitude as predictors correctly classifies only 20 of the 37 hurricanes (54%). A classification tree for Class using the CART-style exhaustive search for univariate splits option correctly classifies all 37 hurricanes. The Tree graph for the classification tree is shown below.

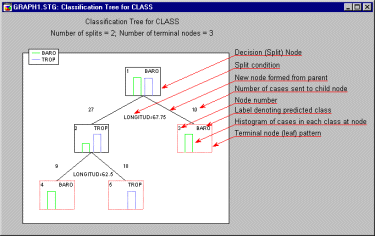
The headings of the graph give the summary information that the classification tree has 2 splits and 3 terminal nodes. Terminal nodes, or terminal leaves as they are sometimes called, are points on the tree beyond which no further decisions are made. In the graph itself, terminal nodes are outlined with dotted red lines, while the remaining decision nodes or split nodes are outlined with solid black lines. The tree starts with the top decision node, sometimes called the root node. In the graph it is labeled as node 1 in its top-left corner. Initially, all 37 hurricanes are assigned to the root node and tentatively classified as Baro hurricanes, as indicated by the Baro label in the top-right corner of the root node. Baro is chosen as the initial classification because there are slightly more Baro than Trop hurricanes, as indicated by the histogram plotted within the root node. The legend identifying which bars in the node histograms correspond to Baro and Trop hurricanes is located in the top-left corner of the graph.
The root node is split, forming two new nodes. The text below the root node describes the split. It indicates that hurricanes with Longitude coordinate values of less than or equal to 67.75 are sent to node number 2 and tentatively classified as Trop hurricanes, and that hurricanes with Longitude coordinate values of greater than 67.75 are assigned to node number 3 and classified as Baro hurricanes. The values of 27 and 10 printed above nodes 2 and 3, respectively, indicate the number of cases sent to each of these two child nodes from their parent, the root node. Similarly, node 2 is subsequently split. The split is such that the 9 hurricanes with Longitude coordinate values of less than or equal to 62.5 are sent to node number 4 and classified as Baro hurricanes, and the remaining 18 hurricanes with Longitude coordinate values of greater than 62.5 are sent to node number 5 and classified as Trop hurricanes.
The Tree graph presents all this information in a simple, straightforward way, and probably allows one to digest the information in much less time than it takes to read the two preceding paragraphs. Getting to the bottom line, the histograms plotted within the tree's terminal nodes show that the classification tree classifies the hurricanes perfectly. Each of the terminal nodes is "pure," containing no misclassified hurricanes. All the information in the Tree graph is also available in the Tree structure Scrollsheet shown below.
| Tree Structure (barotrop.sta) | |||||||
|---|---|---|---|---|---|---|---|
| CLASSIF. TREES |
Child nodes, observed class n's, predicted class, and split condition for each node |
||||||
| Node |
Left branch |
Right branch |
n in cls BARO |
n in cls TROP |
Predict. class |
Split constant |
Split variable |
| 1 2 3 4 5 |
2 4 |
3 5 |
19 9 10 9 0 |
18 18 0 0 18 |
BARO TROP BARO BARO TROP |
-67.75 -62.50 |
LONGITUD LONGITUD |
Note that in the Scrollsheet nodes 3 through 5 are identified as terminal nodes because no split is performed at those nodes. Also note the signs of the Split constants displayed in the Scrollsheet, for example, -67.75 for the split at node 1. In the Tree graph, the split condition at node 1 is described as LONGITUD 67.75 rather than as (the equivalent) -67.75 + LONGITUD 0. This is done simply to save space on the graph.
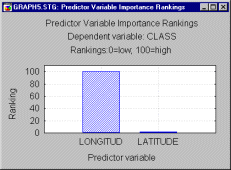
When univariate splits are performed, the predictor variables can be ranked on a 0 - 100 scale in terms of their potential importance in accounting for responses on the dependent variable. For this example, Longitude is clearly very important and Latitude is relatively unimportant.
A classification tree Class using the Discriminant-based univariate split selection method option produces similar results. The Tree structure Scrollsheet shown for this analysis shows that the splits of -63.4716 and -67.7516 are quite similar to the splits found using the CART-style exhaustive search for univariate splits option, although 1 Trop hurricane in terminal node 2 is misclassified as Baro.
| Tree Structure (barotrop.sta) | |||||||
|---|---|---|---|---|---|---|---|
| CLASSIF. TREES |
Child nodes, observed class n's, predicted class, and split condition for each node |
||||||
| Node |
Left branch |
Right branch |
n in cls BARO |
n in cls TROP |
Predict. class |
Split constant |
Split variable |
| 1 2 3 4 5 |
2 4 |
3 5 |
19 9 10 0 10 |
18 1 17 17 0 |
BARO BARO TROP TROP BARO |
-63.4716 -67.7516 |
LONGITUD LONGITUD |
A categorized scatterplot for Longitude and Latitude clearly shows why linear discriminant analysis fails so miserably at predicting Class, and why the classification tree succeeds so well.
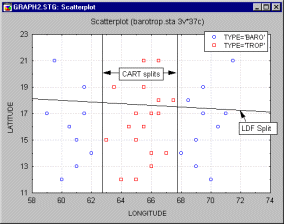
The plot clearly shows that there is no strong linear relationship of longitude or latitude coordinates with Class, or of any possible linear combination of longitude and latitude with Class. Class is not functionally related to longitude or latitude, at least in the linear sense. The LDF (Linear Discriminant Function) Split shown on the graph is almost a "shot in the dark" at trying to separate predicted Trop hurricanes (above the split line) from predicted Baro hurricanes (below the split line). The CART univariate splits, because they are not restricted to a single linear combination of longitude and latitude scores, find the "cut points" on the Longitude dimension that allow the best possible (in this case, perfect) classification of hurricane Class.
Now we can examine a situation illustrating the pitfalls of classification tree. Suppose that the following hurricane data were available.
| DATA: Barotro2.sta 3v | ||
|---|---|---|
| LONGITUD | LATITUDE | CLASS |
| 59.00 59.50 60.00 60.50 61.00 61.00 61.50 61.50 62.00 63.00 63.50 64.00 64.50 65.00 65.00 65.00 65.50 65.50 65.50 66.00 66.00 66.00 66.50 66.50 66.50 67.00 67.50 68.00 68.50 69.00 69.00 69.50 69.50 70.00 70.50 71.00 71.50 |
17.00 21.00 12.00 16.00 13.00 15.00 17.00 19.00 14.00 15.00 19.00 12.00 16.00 12.00 15.00 17.00 16.00 19.00 21.00 13.00 14.00 17.00 17.00 18.00 21.00 14.00 18.00 14.00 18.00 13.00 15.00 17.00 19.00 12.00 16.00 17.00 21.00 |
BARO BARO TROP BARO TROP TROP BARO BARO TROP TROP BARO TROP TROP TROP TROP BARO TROP BARO BARO TROP TROP BARO BARO BARO BARO TROP BARO TROP BARO TROP TROP TROP BARO TROP TROP TROP BARO |
A linear discriminant analysis of hurricane Class (Baro or Trop) using Longitude and Latitude as predictors correctly classifies all 37 of the hurricanes. A classification tree analysis for Class using the CART-style exhaustive search for univariate splits option also correctly classifies all 37 hurricanes, but the tree requires 5 splits producing 6 terminal nodes. Which results are easier to interpret? In the linear discriminant analysis, the raw canonical discriminant function coefficients for Longitude and Latitude on the (single) discriminant function are .122073 and -.633124, respectively, and hurricanes with higher longitude and lower latitude coordinates are classified as Trop. The interpretation would be that hurricanes in the western Atlantic at low latitudes are likely to be Trop hurricanes, and that hurricanes further east in the Atlantic at higher latitudes are likely to be Baro hurricanes.
The Tree graph for the classification tree analysis using the CART-style exhaustive search for univariate splits option is shown below.
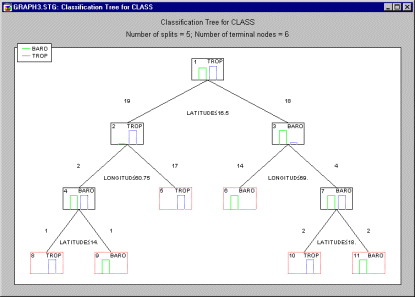
One could methodically describe the splits in this classification tree, exactly as was done in the previous example, but because there are so many splits, the interpretation would necessarily be more complex than the simple interpretation provided by the single discriminant function from the linear discrimination analysis.
However, recall that in describing the flexibility of Classification Trees , it was noted that an option exists for Discriminant-based linear combination splits for ordered predictors using algorithms from QUEST. The Tree graph for the classification tree analysis using linear combination splits is shown below.
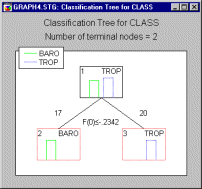
Note that in this tree, just one split yields perfect prediction. Each of the terminal nodes is "pure," containing no misclassified hurricanes. The linear combination split used to split the root node into its left child node and right child node is summarized by the description "F(0) -.2342." This indicates that if a hurricane has a score of less than or equal to -.2342 on the split function--abbreviated as F(0)--then it is sent to the left child node and classified as Baro, otherwise it is sent to the right child node and classified as Trop. The split function coefficients (.011741 for Longitude and -.060896 for Latitude) have the same signs and are similar in their relative magnitude to the corresponding linear discriminant function coefficients from the linear discriminant analysis, so the two analyses are functionally identical, at least in terms of their predictions of hurricane Class.
The moral of this story of the power and pitfalls of classification trees is that classification trees are only as good as the choice of analysis option used to produce them. For finding models that predict well, there is no substitute for a thorough understanding of the nature of the relationships between the predictor and dependent variables.
We have seen that classification trees analysis can be characterized as a hierarchical, highly flexible set of techniques for predicting membership of cases or objects in the classes of a categorical dependent variable from their measurements on one or more predictor variables. With this groundwork behind us, we now are ready to look at the methods for computing classification trees in greater detail.
For information on the basic purpose of classification trees, see Basic Ideas. See also, Exploratory Data Analysis and Data Mining Techniques.
| To index |
Computational Methods
The process of computing classification trees can be characterized as involving four basic steps:
Specifying the Criteria for Predictive Accuracy
The goal of classification tree analysis, simply stated, is to obtain the most accurate prediction possible. Unfortunately, an operational definition of accurate prediction is hard to come by. To solve the problem of defining predictive accuracy, the problem is "stood on its head," and the most accurate prediction is operationally defined as the prediction with the minimum costs. The term costs need not seem mystifying. In many typical applications, costs simply correspond to the proportion of misclassified cases. The notion of costs was developed as a way to generalize, to a broader range of prediction situations, the idea that the best prediction has the lowest misclassification rate.
The need for minimizing costs, rather than just the proportion of misclassified cases, arises when some predictions that fail are more catastrophic than others, or when some predictions that fail occur more frequently than others. The costs to a gambler of losing a single bet (or prediction) on which the gambler's whole fortune is at stake are greater than the costs of losing many bets (or predictions) on which a tiny part of the gambler's fortune is at stake. Conversely, the costs of losing many small bets can be larger than the costs of losing just a few bigger bets. One should spend proportionately more effort in minimizing losses on bets where losing (making errors in prediction) costs you more.
Priors. Minimizing costs, however, does correspond to minimizing the proportion of misclassified cases when Priors are taken to be proportional to the class sizes and when Misclassification costs are taken to be equal for every class. We will address Priors first. Priors, or, a priori probabilities, specify how likely it is, without using any prior knowledge of the values for the predictor variables in the model, that a case or object will fall into one of the classes. For example, in an educational study of high school drop-outs, it may happen that, overall, there are fewer drop-outs than students who stay in school (i.e., there are different base rates); thus, the a priori probability that a student drops out is lower than that a student remains in school.
The a priori probabilities used in minimizing costs can greatly affect the classification of cases or objects. If differential base rates are not of interest for the study, or if one knows that there are about an equal number of cases in each class, then one would use equal priors. If the differential base rates are reflected in the class sizes (as they would be, if the sample is a probability sample) then one would use priors estimated by the class proportions of the sample. Finally, if you have specific knowledge about the base rates (for example, based on previous research), then one would specify priors in accordance with that knowledge. For example, a priori probabilities for carriers of a recessive gene could be specified as twice as high as for individuals who display a disorder caused by the recessive gene. The general point is that the relative size of the priors assigned to each class can be used to "adjust" the importance of misclassifications for each class. Minimizing costs corresponds to minimizing the overall proportion of misclassified cases when Priors are taken to be proportional to the class sizes (and Misclassification costs are taken to be equal for every class), because prediction should be better in larger classes to produce an overall lower misclassification rate.
Misclassification costs. Sometimes more accurate classification is desired for some classes than others for reasons unrelated to relative class sizes. Regardless of their relative frequency, carriers of a disease who are contagious to others might need to be more accurately predicted than carriers of the disease who are not contagious to others. If one assumes that little is lost in avoiding a non-contagious person but much is lost in not avoiding a contagious person, higher misclassification costs could be specified for misclassifying a contagious carrier as non-contagious than for misclassifying a non-contagious person as contagious. But to reiterate, minimizing costs corresponds to minimizing the proportion of misclassified cases when Priors are taken to be proportional to the class sizes and when Misclassification costs are taken to be equal for every class.
Case weights. A little less conceptually, the use of case weights on a weighting variable as case multipliers for aggregated data sets is also related to the issue of minimizing costs. Interestingly, as an alternative to using case weights for aggregated data sets, one could specify appropriate priors and/or misclassification costs and produce the same results while avoiding the additional processing required to analyze multiple cases with the same values for all variables. Suppose that in an aggregated data set with two classes having an equal number of cases, there are case weights of 2 for all the cases in the first class, and case weights of 3 for all the cases in the second class. If you specify priors of .4 and .6, respectively, specify equal misclassification costs, and analyze the data without case weights, you will get the same misclassification rates as you would get if you specify priors estimated by the class sizes, specify equal misclassification costs, and analyze the aggregated data set using the case weights. You would also get the same misclassification rates if you specify priors to be equal, specify the costs of misclassifying class 1 cases as class 2 cases to be 2/3 of the costs of misclassifying class 2 cases as class 1 cases, and analyze the data without case weights.
The relationships between priors, misclassification costs, and case weights become quite complex in all but the simplest situations (for discussions, see Breiman et al, 1984; Ripley, 1996). In analyses where minimizing costs corresponds to minimizing the misclassification rate, however, these issues need not cause any concern. Priors, misclassification costs, and case weights are brought up here, however, to illustrate the wide variety of prediction situations that can be handled using the concept of minimizing costs, as compared to the rather limited (but probably typical) prediction situations that can be handled using the narrower (but simpler) idea of minimizing misclassification rates. Furthermore, minimizing costs is an underlying goal of classification tree analysis, and is explicitly addressed in the fourth and final basic step in classification tree analysis, where in trying to select the "right-sized" tree, one chooses the tree with the minimum estimated costs. Depending on the type of prediction problem you are trying to solve, understanding the idea of reduction of estimated costs may be important for understanding the results of the analysis.
Selecting Splits
The second basic step in classification tree analysis is to select the splits on the predictor variables which are used to predict membership in the classes of the dependent variables for the cases or objects in the analysis. Not surprisingly, given the hierarchical nature of classification trees, these splits are selected one at time, starting with the split at the root node, and continuing with splits of resulting child nodes until splitting stops, and the child nodes which have not been split become terminal nodes. Three Split selection methods are discussed here.
Discriminant-based univariate splits. The first step in split selection when the Discriminant-based univariate splits option is chosen is to determine the best terminal node to split in the current tree, and which predictor variable to use to perform the split. For each terminal node, p-levels are computed for tests of the significance of the relationship of class membership with the levels of each predictor variable. For categorical predictors, the p-levels are computed for Chi-square tests of independence of the classes and the levels of the categorical predictor that are present at the node. For ordered predictors, the p-levels are computed for ANOVAs of the relationship of the classes to the values of the ordered predictor that are present at the node. If the smallest computed p-level is smaller than the default Bonferoni-adjusted p-level for multiple comparisons of .05 (a different threshold value can be used), the predictor variable producing that smallest p-level is chosen to split the corresponding node. If no p-level smaller than the threshold p-level is found, p-levels are computed for statistical tests that are robust to distributional violations, such as Levene's F. Details concerning node and predictor variable selection when no p-level is smaller than the specified threshold are described in Loh and Shih (1997).
The next step is to determine the split. For ordered predictors, the 2-means clustering algorithm of Hartigan and Wong (1979, see also Cluster Analysis) is applied to create two "superclasses" for the node. The two roots are found for a quadratic equation describing the difference in the means of the "superclasses" on the ordered predictor, and the values for a split corresponding to each root are computed. The split closest to a "superclass" mean is selected. For categorical predictors, dummy-coded variables representing the levels of the categorical predictor are constructed, and then singular value decomposition methods are applied to transform the dummy-coded variables into a set of non-redundant ordered predictors. The procedures for ordered predictors are then applied and the obtained split is "mapped back" onto the original levels of the categorical variable and represented as a contrast between two sets of levels of the categorical variable. Again, further details about these procedures are described in Loh and Shih (1997). Although complicated, these procedures reduce a bias in split selection that occurs when using the CART-style exhaustive search method for selecting splits. This is the bias toward selecting variables with more levels for splits, a bias which can skew the interpretation of the relative importance of the predictors in explaining responses on the dependent variable (Breiman et. al., 1984).
Discriminant-based linear combination splits. The second split selection method is the Discriminant-based linear combination split option for ordered predictor variables (however, the predictors are assumed to be measured on at least interval scales). Surprisingly, this method works by treating the continuous predictors from which linear combinations are formed in a manner which is similar to the way categorical predictors are treated in the previous method. Singular value decomposition methods are used to transform the continuous predictors into a new set of non-redundant predictors. The procedures for creating "superclasses" and finding the split closest to a "superclass" mean are then applied, and the results are "mapped back" onto the original continuous predictors and represented as a univariate split on a linear combination of predictor variables.
CART-style exhaustive search for univariate splits. The third split-selection method is the CART-style exhaustive search for univariate splits method for categorical or ordered predictor variables. With this method, all possible splits for each predictor variable at each node are examined to find the split producing the largest improvement in goodness of fit (or equivalently, the largest reduction in lack of fit). What determines the domain of possible splits at a node? For categorical predictor variables with k levels present at a node, there are 2(k-1) - 1 possible contrasts between two sets of levels of the predictor. For ordered predictors with k distinct levels present at a node, there are k -1 midpoints between distinct levels. Thus it can be seen that the number of possible splits that must be examined can become very large when there are large numbers of predictors with many levels which must be examined at many nodes.
How is improvement in goodness of fit determined? Three choices of Goodness of fit measures are discussed here. The Gini measure of node impurity is a measure which reaches a value of zero when only one class is present at a node (with priors estimated from class sizes and equal misclassification costs, the Gini measure is computed as the sum of products of all pairs of class proportions for classes present at the node; it reaches its maximum value when class sizes at the node are equal). The Gini measure was the measure of goodness of fit preferred by the developers of CART (Breiman et. al., 1984). The two other indices are the Chi-square measure, which is similar to Bartlett's Chi-square (Bartlett, 1948), and the G-square measure, which is similar to the maximum-likelihood Chi-square used in structural equation modeling. The CART-style exhaustive search for univariate splits method works by searching for the split that maximizes the reduction in the value of the selected goodness of fit measure. When the fit is perfect, classification is perfect.
Determining When to Stop Splitting
The third step in classification tree analysis is to determine when to stop splitting. One characteristic of classification trees is that if no limit is placed on the number of splits that are performed, eventually "pure" classification will be achieved, with each terminal node containing only one class of cases or objects. However, "pure" classification is usually unrealistic. Even a simple classification tree such as a coin sorter can produce impure classifications for coins whose sizes are distorted or if wear changes the lengths of the slots cut in the track. This potentially could be remedied by further sorting of the coins that fall into each slot, but to be practical, at some point the sorting would have to stop and you would have to accept that the coins have been reasonably well sorted.
Likewise, if the observed classifications on the dependent variable or the levels on the predicted variable in a classification tree analysis are measured with error or contain "noise," it is unrealistic to continue to sort until every terminal node is "pure." Two options for controlling when splitting stops will be discussed here. These two options are linked to the choice of the Stopping rule specified for the analysis.
Minimum n. One option for controlling when splitting stops is to allow splitting to continue until all terminal nodes are pure or contain no more than a specified minimum number of cases or objects. The desired minimum number of cases can be specified as the Minimum n, and splitting will stop when all terminal nodes containing more than one class have no more than the specified number of cases or objects.
Fraction of objects. Another option for controlling when splitting stops is to allow splitting to continue until all terminal nodes are pure or contain no more cases than a specified minimum fraction of the sizes of one or more classes. The desired minimum fraction can be specified as the Fraction of objects and, if the priors used in the analysis are equal and class sizes are equal, splitting will stop when all terminal nodes containing more than one class have no more cases than the specified fraction of the class sizes for one or more classes. If the priors used in the analysis are not equal, splitting will stop when all terminal nodes containing more than one class have no more cases than the specified fraction for one or more classes.
Selecting the "Right-Sized" Tree
After a night at the horse track, a studious gambler computes a huge classification tree with numerous splits that perfectly account for the win, place, show, and no show results for every horse in every race. Expecting to become rich, the gambler takes a copy of the Tree graph to the races the next night, sorts the horses racing that night using the classification tree, makes his or her predictions and places his or her bets, and leaves the race track later much less rich than had been expected. The poor gambler has foolishly assumed that a classification tree computed from a learning sample in which the outcomes are already known will perform equally well in predicting outcomes in a second, independent test sample. The gambler's classification tree performed poorly during cross-validation. The gambler's payoff might have been larger using a smaller classification tree that did not classify perfectly in the learning sample, but which was expected to predict equally well in the test sample.
Some generalizations can be offered about what constitutes the "right-sized" classification tree. It should be sufficiently complex to account for the known facts, but at the same time it should be as simple as possible. It should exploit information that increases predictive accuracy and ignore information that does not. It should, if possible, lead to greater understanding of the phenomena which it describes. Of course, these same characteristics apply to any scientific theory, so we must try to be more specific about what constitutes the "right-sized" classification tree. One strategy is to grow the tree to just the right size, where the right size is determined by the user from knowledge from previous research, diagnostic information from previous analyses, or even intuition. The other strategy is to use a set of well-documented, structured procedures developed by Breiman et al. (1984) for selecting the "right-sized" tree. These procedures are not foolproof, as Breiman et al. (1984) readily acknowledge, but at least they take subjective judgment out of the process of selecting the "right-sized" tree.
FACT-style direct stopping. We will begin by describing the first strategy, in which the researcher specifies the size to grow the classification tree. This strategy is followed by using FACT-style direct stopping as the Stopping rule for the analysis, and by specifying the Fraction of objects which allows the tree to grow to the desired size. There are several options for obtaining diagnostic information to determine the reasonableness of the choice of size for the tree. Three options for performing cross-validation of the selected classification tree are discussed below.
Test sample cross-validation. The first, and most preferred type of cross-validation is test sample cross-validation. In this type of cross-validation, the classification tree is computed from the learning sample, and its predictive accuracy is tested by applying it to predict class membership in the test sample. If the costs for the test sample exceed the costs for the learning sample (remember, costs equal the proportion of misclassified cases when priors are estimated and misclassification costs are equal), this indicates poor cross-validation and that a different sized tree might cross-validate better. The test and learning samples can be formed by collecting two independent data sets, or if a large learning sample is available, by reserving a randomly selected proportion of the cases, say a third or a half, for use as the test sample.
V-fold cross-validation. This type of cross-validation is useful when no test sample is available and the learning sample is too small to have the test sample taken from it. A specified V value for V-fold cross-validation determines the number of random subsamples, as equal in size as possible, that are formed from the learning sample. The classification tree of the specified size is computed V times, each time leaving out one of the subsamples from the computations, and using that subsample as a test sample for cross-validation, so that each subsample is used V - 1 times in the learning sample and just once as the test sample. The CV costs computed for each of the V test samples are then averaged to give the V-fold estimate of the CV costs.
Global cross-validation. In global cross-validation, the entire analysis is replicated a specified number of times holding out a fraction of the learning sample equal to 1 over the specified number of times, and using each hold-out sample in turn as a test sample to cross-validate the selected classification tree. This type of cross-validation is probably no more useful than V-fold cross-validation when FACT-style direct stopping is used, but can be quite useful as a method validation procedure when automatic tree selection techniques are used (for discussion, see Breiman et. al., 1984). This brings us to the second of the two strategies that can used to select the "right-sized" tree, an automatic tree selection method based on a technique developed by Breiman et al. (1984) called minimal cost-complexity cross-validation pruning.
Minimal cost-complexity cross-validation pruning. Two methods of pruning can be used depending on the Stopping Rule you choose to use. Minimal cost-complexity cross-validation pruning is performed when you decide to Prune on misclassification error (as a Stopping rule), and minimal deviance-complexity cross-validation pruning is performed when you choose to Prune on deviance (as a Stopping rule). The only difference in the two options is the measure of prediction error that is used. Prune on misclassification error uses the costs that we have discussed repeatedly (which equal the misclassification rate when priors are estimated and misclassification costs are equal). Prune on deviance uses a measure, based on maximum-likelihood principles, called the deviance (see Ripley, 1996). We will focus on cost-complexity cross-validation pruning (as originated by Breiman et. al., 1984), since deviance-complexity pruning merely involves a different measure of prediction error.
The costs needed to perform cost-complexity pruning are computed as the tree is being grown, starting with the split at the root node up to its maximum size, as determined by the specified Minimum n. The learning sample costs are computed as each split is added to the tree, so that a sequence of generally decreasing costs (reflecting better classification) are obtained corresponding to the number of splits in the tree. The learning sample costs are called resubstitution costs to distinguish them from CV costs, because V-fold cross-validation is also performed as each split is added to the tree. Use the estimated CV costs from V-fold cross-validation as the costs for the root node. Note that tree size can be taken to be the number of terminal nodes, because for binary trees the tree size starts at one (the root node) and increases by one with each added split. Now, define a parameter called the complexity parameter whose initial value is zero, and for every tree (including the first, containing only the root node), compute the value for a function defined as the costs for the tree plus the complexity parameter times the tree size. Increase the complexity parameter continuously until the value of the function for the largest tree exceeds the value of the function for a smaller-sized tree. Take the smaller-sized tree to be the new largest tree, continue increasing the complexity parameter continuously until the value of the function for the largest tree exceeds the value of the function for a smaller-sized tree, and continue the process until the root node is the largest tree. (Those who are familiar with numerical analysis will recognize the use of a penalty function in this algorithm. The function is a linear combination of costs, which generally decrease with tree size, and tree size, which increases linearly. As the complexity parameter is increased, larger trees are penalized for their complexity more and more, until a discrete threshold is reached at which a smaller-sized tree's higher costs are outweighed by the largest tree's higher complexity)
The sequence of largest trees obtained by this algorithm have a number of interesting properties. They are nested, because successively pruned trees contain all the nodes of the next smaller tree in the sequence. Initially, many nodes are often pruned going from one tree to the next smaller tree in the sequence, but fewer nodes tend to be pruned as the root node is approached. The sequence of largest trees is also optimally pruned, because for every size of tree in the sequence, there is no other tree of the same size with lower costs. Proofs and/or explanations of these properties can be found in Breiman et al. (1984).
Tree selection after pruning. We now select the "right-sized" tree from the sequence of optimally pruned trees. A natural criterion is the CV costs. While there is nothing wrong with choosing the tree with the minimum CV costs as the "right-sized" tree, oftentimes there will be several trees with CV costs close to the minimum. Breiman et al. (1984) make the reasonable suggestion that one should choose as the "right-sized" tree the smallest-sized (least complex) tree whose CV costs do not differ appreciably from the minimum CV costs. They proposed a "1 SE rule" for making this selection, i.e., choose as the "right-sized" tree the smallest-sized tree whose CV costs do not exceed the minimum CV costs plus 1 times the Standard error of the CV costs for the minimum CV costs tree.
One distinct advantage of the "automatic" tree selection procedure is that it helps to avoid "overfitting" and "underfitting" of the data. The graph below shows a typical plot of the Resubstitution costs and CV costs for the sequence of successively pruned trees.
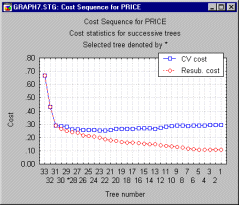
As shown in this graph, the Resubstitution costs (e.g., the misclassification rate in the learning sample) rather consistently decrease as tree size increases. The CV costs, on the other hand, approach the minimum quickly as tree size initially increases, but actually start to rise as tree size becomes very large. Note that the selected "right-sized" tree is close to the inflection point in the curve, that is, close to the point where the initial sharp drop in CV costs with increased tree size starts to level out. The "automatic" tree selection procedure is designed to select the simplest (smallest) tree with close to minimum CV costs, and thereby avoid the loss in predictive accuracy produced by "underfitting" or "overfitting" the data (note the similarity to the logic underlying the use of a "scree plot" to determine the number of factors to retain in Factor Analysis; see also Reviewing the Results of a Principal Components Analysis).
As has been seen, minimal cost-complexity cross-validation pruning and subsequent "right-sized" tree selection is a truly "automatic" process. The algorithms make all the decisions leading to selection of the "right-sized" tree, except for, perhaps, specification of a value for the SE rule. One issue that arises with the use of such "automatic" procedures is how well the results replicate, where replication might involve the selection of trees of quite different sizes across replications, given the "automatic" selection process that is used. This is where global cross-validation can be very useful. As explained previously, in global cross-validation, the entire analysis is replicated a specified number of times (3 is the default) holding out a fraction of the cases to use as a test sample to cross-validate the selected classification tree. If the average of the costs for the test samples, called the global CV costs, exceeds the CV costs for the selected tree, or if the standard error of the global CV costs exceeds the standard error of the CV costs for the selected tree, this indicates that the "automatic" tree selection procedure is allowing too much variability in tree selection rather than consistently selecting a tree with minimum estimated costs.
Classification trees and traditional methods. As can be seen in the methods used in computing classification trees, in a number of respects classification trees are decidedly different from traditional statistical methods for predicting class membership on a categorical dependent variable. They employ a hierarchy of predictions, with many predictions sometimes being applied to particular cases, to sort the cases into predicted classes. Traditional methods use simultaneous techniques to make one and only one class membership prediction for each and every case. In other respects, such as having as its goal accurate prediction, classification tree analysis is indistinguishable from traditional methods. Time will tell if classification tree analysis has enough to commend itself to become as accepted as the traditional methods.
For information on the basic purpose of classification trees, see Basic Ideas. For information on the hierarchical nature and flexibility of classification trees, see Characteristics of Classification Trees. See also, Exploratory Data Analysis and Data Mining Techniques.
| To index |
A Brief Comparison of Classification Tree Programs
A variety of classification tree programs have been developed to predict membership of cases or objects in the classes of a categorical dependent variable from their measurements on one or more predictor variables. In the previous section, Computational Methods, we have discussed the QUEST (Loh & Shih, 1997) and CART (Breiman et. al., 1984) programs for computing binary classification trees based on univariate splits for categorical predictor variables, ordered predictor variables (measured on at least an ordinal scale), or a mix of both types of predictors. We have also discussed computing classification trees based on linear combination splits for interval scale predictor variables.
Some classification trees programs, such as FACT (Loh & Vanichestakul, 1988) and THAID (Morgan & Messenger, 1973, as well as the related programs AID, for Automatic Interaction Detection, Morgan & Sonquist, 1963, and CHAID, for Chi-Square Automatic Interaction Detection, Kass, 1980) perform multi-level splits rather than binary splits when computing classification trees. A multi-level split performs k - 1 splits (where k is the number of levels of the splittting variable), as compared to a binary split which performs one split (regardless of the number of levels of the splittting variable). However, it should be noted that there is no inherent advantage of multi-level splits, because any multi-level split can be represented as a series of binary splits, and there may be disadvantages of using multi-level splits. With multi-level splits, predictor variables can be used for splitting only once, so the resulting classification trees may be unrealistically short and uninteresting (Loh & Shih, 1997). A more serious problem is bias in variable selection for splits. This bias is possible in any program such as THAID (Morgan & Sonquist, 1973) that employs an exhaustive search for finding splits (for a discussion, see Loh & Shih, 1997). Bias in variable selection is the bias toward selecting variables with more levels for splits, a bias which can skew the interpretation of the relative importance of the predictors in explaining responses on the dependent variable (Breiman et. al., 1984).
Bias in variable selection can be avoided by using the Discriminant-based (univariate or linear combination) split options. These options make use of the algorithms in QUEST (Loh & Shih, 1997) to prevent bias in variable selection. The CART-style exhaustive search for univariate splits option is useful if one's goal is to find splits producing the best possible classification in the learning sample (but not necessarily in independent cross-validiation samples). For reliable splits, as well as computational speed, the Discriminant-based split options are recommended.
For information on techniques and issues in computing classification trees, see the Computational Methods section.