ABSTRACT
Thesis Advisors:
Donald W. Schwendeman
and
Julian D. Cole
Department of Mathematical Sciences
Rensselaer Polytechnic Institute
The existence of shock-free flow around a slender body of revolution at
near-sonic speeds is investigated using transonic small-disturbance theory.
The governing partial differential equation, known as the Ká rmá n-Guderley equation, and the boundary conditions are transformed into the
hodograph plane.
In the hodograph plane the spatial variables depend on the velocity components.
The problem is solved numerically, employing an algorithm that involves a
combination of finite-difference and iterative methods.
A condition dependent upon the Jacobian of the transformation is developed to
determine when a shock-free solution has been computed.
A number of bodies possessing shock-free flows are calculated at different
values of the transonic similarity parameter, K = (1 - M
)/(M 
),
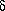
where M is the flow Mach number and 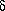is the body thickness.
The body profiles computed are both fore-aft symmetric and fore-aft asymmetric.
For moderate values of K (e.g. K = 3.5, corresponding to M = 0.985
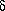and = 0.1) there is little difficulty in finding shock-free
solutions in the hodograph. Solutions have not been calculated for K less than
about 3, corresponding to speeds very close to sonic.
Calculations in the physical plane of the flow around transonic slender
bodies of revolution are performed at moderate values of K in order to
confirm the shock-free nature of the body profiles obtained from the hodograph
calculations and to explore off-design conditions.
It is found that the flow field in the physical plane around the shock-free
hodograph-designed bodies appears to be nearly shock-free,
having at most a weak shock. Small perturbations to K or to the hodograph-designed
body shape do not appear to create qualitatively different flow fields.
The numerical evidence suggests that shock-free flows are isolated but
that nearby flows possess, at most, weak shocks.