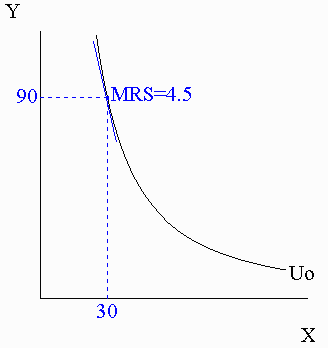II. CONSUMER DEMAND
A. THE RATIONAL CONSUMER
2. CONSUMER PREFERENCES AND
INDIFFERENCE CURVES (Uo)
We've set up the consumer's constraints which
establish consumption possibilities
Now we turn to preferences to see what choices the consumer will make
a. BASIC CONCEPTS
Focus is on pure consumption: use it or lose it, but
you have free disposability (you can throw away but not sell what you don't consume)
For any bundles A and B, a consumer
is able to decide:
"I prefer A to B."
"I prefer B to A."
"I am indifferent between A and B."
These preferences are: (1) complete,
(2) stable, and (3) transitive
Concept related to total utility: Marginal Utility (MU): the
increase in total utility due to the consumption of one extra unit of some item, holding
all else constant:
MUx = DU/DX
MUy = DU/DY
Example: You consume donuts (D) and
milk (M).
Milk consumption rises with your quantity of donuts fixed
Property (1) of utility: the MU of any economic good is positive.
MUx > 0. (more is better)
Property (2) of utility: MU falls as
consumption rises
("law of diminishing marginal utility)."
As with the budget line for consumer constraints, to
illustrate consumer decisionmaking for more than one item, we need to be able to
incorporate consumer utility into our x-y diagram. That's our next step.
b.
GEOMETRY
Indifference curves: Arise when
consumers face a choice and respond, "I don't care which I choose."
Indifference curve:
a set of consumption bundles that a consumer regards as equally desirable.
| Example: milk and donuts. Along the indifference curve,
U(M,D) = Uo,
where Uo is a constant.
? Where in the diagram are
consumption bundles that you would not like as much as the bundles along Uo?
Bundles below Uo are less desirable to you--they have
less of milk and/or donuts than the points along Uo.
Note that a single indifference curve divides up an entire consumption
set into more preferred and less preferred consumption bundles.
Indifference map: a set of several
indifference curves. |
 |
 |
|
Note: Utility = real income
=> all along Uo, real income is constant.
(The consumer is equally happy even though the consumption bundles and
their money costs differ.)
Examples of indifference
curves:
Worksheet
Think each case through and don't be surprised if these curves have
rather unusual shapes compared to the
'typical' curves we covered in the basic geometry.
Illustrations of worksheet examples
(Java)
The Marginal Rate of Substitution
(MRS)
(handout: The Marginal Rate of Substitution (MRS))
(1) the geometry of the MRS
Consider points A and B on
Uo:
Milk
Donuts
A 1 10
B 2 5
? How has each of the following changed in the move FROM A to B?
? Milk consumption? DM =
? Donut consumption? DD =
? Utility? DU =
The consumer has substituted 1 glass of milk for 5
donuts and is just as well off as before.
In general, the slope of an indifference curve tells us the rate at
which good X can substitute for good Y without affecting utility. |
|
 |
|
The MRS = the maximum amount of good
Y (here donuts) which a consumer is willing to give up for another unit of good X (here
milk).
Geometry: MRS= the size of the slope of an indifference curve.
Here: MRS = 5 => consumer is
willing to give up 5 donuts for 1milk.
MRS tells you the value of X relative
to Y.
Now let's take a closer look at the slope of a
typical indifference curve, the curve's marginal rate of substitution.
(2) the mathematics of the MRS
Recall: Px and Py determine the slope of the BL
(OppCost)
The analogy here: MUx and MUy
determine the slope of Uo
Even though we can’t directly measure MUs, we
can show that they do determine the slope of Uo.
DU = MUx.DX + MUy.DY
Along Uo, DU = 0 =>
-MUy.DY = MUx.DX
Rearrange terms:
|-DY|
MUx
-------- = -------- ( = MRS)
| DX|
MUy
(3) the logic of the MRS
  |
General case: |
| |
Example here: |
|
MUx = utility gained from an
extra X |
| |
MUx = 10 utils |
|
MUy = rate utility falls when
giving up Y |
| |
MUy = 2 utils |
|
 |
| |
|
|
=> MUx/MUy |
| |
10u/(2u per Y) |
|
= total Y you can give up for
1X w/o losing utility |
| |
5Y for 1X |
|
= |-DY/DX| (the size
of the slope of Uo) |
| |
|
The more satisfying (i.e., valuable) milk is compared
to donuts, the more donuts a consumer will give up to get that milk.
So Uo will be steep when milk is valued highly compared to donuts, flat
when milk is not so highly valued compared to donuts.
Resume day 7
Summary: comparing BL and Uo
Slope of BL reflects the price of X relative to Y
Slope of Uo reflects the value of X relative to Y
c. PROPERTIES OF INDIFFERENCE
CURVES
4 key properties to indifference
curves:
(online review: properties of indifference curves
(Java))
Property (1): Every consumption point
is on some indifference curve.
(Indifference curves can
be "thick"--for example, if you don't consume either item)
Property (2): Indifference curves for
economic goods slope down.
(reflects your
willingness to trade off items you like)
? Would an
individual's indifference curves surprise you if they looked like the ones shown here?
? Why or why not?
? What property could we state to avoid this problem?
Property (3): An individual's
indifference curves never cross. |
 |
 |
|
| The last property pertains
to the curvature of Uo:
Property (4): Indifference curves for goods are convex to the origin.
To see why, consider the following four points along
Uo:
Point Milk Donuts
A 1 10
A' 2 5
B 4 2.5
B' 5 2 |
 |
 |
|
At point A you have lots of donuts and little milk
(1,10).
At A: You place a high value on
more milk (MRS=5)
(5D for 1M, moving you to point A').
At B, you have more milk and fewer donuts.
At B: You place a lower value on
even more milk (MRS=0.5)
(1/2D for 1M, moving you to point B').
So notice that the marginal value you place on a good
depends on how much you already have.
The econ version of the relativity theory of value:
Examples:
diamond/water paradox
beads for manhattan
frequency of a 3d child
(56% for (0,2) v. 51% for (1,1))
The 2 limits to indifference curve
convexity are (1) perfect complements and (2) perfect substitutes
Application: Joyce brothers example
? Preface: What is the derivative of
a power function? y = B0xB1?
Ordinarily, we have smooth, convex downward-sloping
indifference curves.
For specificity, what sort of utility function would give us that
result?
One common one is...
The most commonly used utility
function: Cobb-Douglas utility function:
U = a.XBxYBy
Worksheet
Key result: For a Cobb-Douglas
utility function:
Bx Y
MRS = ---- . ---
By X
which falls continuously as we move down an indifference
curve (X falls and Y rises).
Numerical
example:
U = X0.6·Y0.4 ? MRS formula =
If Y=90 and X=30:
? MRS value = |
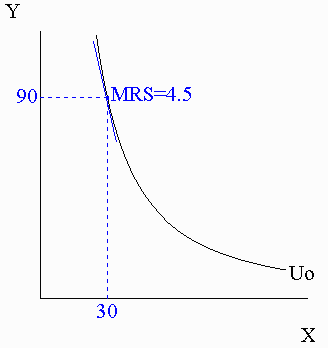 |
Practice MRS with the Utility calculator (Excel)
Next topic