Homework 24: Key

2.	(from Frank, Ch.18): Why are the aggregate willingness-to-pay curves added vertically, not horizontally, to get the aggregate willingness-to-pay curve for a public good? Vertical distance measures marginal benefit of the unit to whomever consumes it. For a private good, only one consumer gets each unit, so we add demands horizontally to compute the quantity demanded at each price. For a public good, many consumers share each unit, so we add the marginal benefits vertically to compute the unit's benefit to all of its consumers.

3.	Suppose that there are two groups (A and B) of potential customers for a cultural programs cable TV channel. Each group consists of 1,000 potential customers with the following demands for cultural programs: PA = 100 - .8(Q), and PB = 24 - .4(Q), with prices measured in dollars. The supply curve for the channel's program is given by PT = 40 + 1.6(Q) where PT denotes the combined price collected from all customers, measured in $1,000.
	a.	How many cultural programs should the channel offer? (Hint: notice that since PA and PB are measured in dollars, the same demand equations measure PA and PB in thousands of dollars for each group of 1,000 consumers, which is the same unit of measurement used for PT in the supply equation.) Q* = 30 PAt = 100-0.8(Q), PBt=24-.4(Q), both Pt's measured in $1,000. Efficiency => Demnad: Pt = 124-1.2(Q) equals supply: 124-1.2(Q) = 40+1.6(Q) => Q=30 programs.
	b.	What should the price per program be for each consumer in Group A? In Group B? How much revenue per program (PT) will the cultural channel collect? PA = 76 PB = 12 PT ($1,000) = 88 ($1000) PA = 100-.8(30)=76; PB=24-.4(30)=12. Channel will collect 88 ($1000) per program.
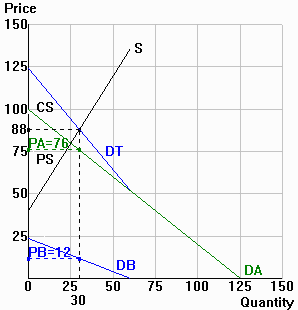
	c.	In the diagram to the right, draw (1) the combined demand curve for the consumers in Group A (DA), (2) the combined demand curve for the consumers in Group B (DB), (3) the combined demand curve of the two groups of consumers (DT) and (4) the supply curve. Measure price in thousands of dollars. (1) = DA; (2) = DB; (3) = DT; (4) = S Answer key checklist: Did you clearly show a vertical sum for DT? (The vertical intercept for DT = the two separate intercepts combined, and since DA and DB have different horizontal intercepts, DT has a kink at the Q where the lower demand curve ends.)
	d.	Indicate in the diagram (1) the equilibrium output, (2) the total price collected, (3) the price collected from each of the two groups of consumers, (4) total consumer surplus and (5) total producer surplus. (1) = 30; (2) = 88; (3) = 12 and 76; (4) = CS (area between DT and P=88 out to 30); (5) = PS (area between P=88 and S out to 30).

1.	Consider the market for used cars. Suppose that the used car market starts out with two types of cars: 50% of used cars = good cars, worth $16,000. 50% of used cars = bad cars, worth $4,000. Only sellers know which car they own.
	a.	What is the expected value of a used car to buyers? Expected value: .5 x $16K + .5 x $4K = $10,000.
	b.	How can the market for used cars end up with a market failure due to adverse selection? Sellers of good cars will not accept the $10,000 offers, so they will leave the market. Only bad cars will be left, selling for $4,000. So the market for good used cars will be eliminated and only the cars with the most adverse characteristics will be marketed.
	c.	In recent years, a market has emerged in which used car owners can market their cars through auto dealers that provide quality certifications with extended warranties. How can this help address the problem caused by asymmetric information? The warranties serve as credible signals that the cars with the warranties are higher quality cars, so they can fetch a higher price. This can restore the market for good used cars.