| 1. |
Suppose that animated films are produced with the
following production function:
Q = K·L where Q = output, K = quantity of
capital, L = quantity of labor. |
|
a. |
What is the exact (point estimate) formula for
the marginal rate of technical substitution (MRTS) for this production function?
MRTS = K/L. |
|
b. |
Suppose the firm wants to produce 12 animated
films (Q=12). Complete columns 3 and 4 of the table below: |
|
|
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
Input
combination |
L |
K |
MRTS |
TC |
PL/PK |
MRTS vs. PL/PK
(>, <, =) |
| a |
1 |
12 |
12 |
5100 |
.75 |
> |
| b |
2 |
6 |
3 |
3000 |
.75 |
> |
| c |
3 |
4 |
1.33 |
2500 |
.75 |
> |
| d |
4 |
3 |
.75 |
2400 |
.75 |
= |
| e |
5 |
2.4 |
.48 |
2460 |
.75 |
< |
| f |
6 |
2 |
.33 |
2600 |
.75 |
< |
|
|
c. |
Plot the firm's isoquant for Q=12. Put labor (L) on the
horizontal axis.
See diagram (only the isoquant for now). |
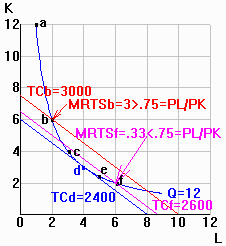 |
|
d. |
Now suppose that the price of labor (PL) = $300 and the price
of capital (PK) = $400. Complete the rest of the table above.
See table above. |
|
e. |
Which input combination satisfies the firm's tangency
condition for producing 12 animated films? How did you decide? Does that combination
minimize the firm's total cost of producing 12 animated films?
Bundle d satisfies T.C.
MRTS = PL/PK.
That bundle does give lowest TC (2400) |
|
f. |
In your diagram from part c, plot the firm's
isocost lines for input combinations b, d, and f, and indicate in your diagram how MRTS
compares to PL/PK at each point.
See diagram: (1) isocost lines for input
combinations b, d, and f, and (2) MRTS vs. PL/PK at each point.
Answer key checklist: Are all your
total cost lines parallel? Is TCd tangent to Q=12? Did you draw TCb>TCf>TCd? |
 |
|
|
|
2. |
Suppose that a rice farmer uses the following
combination of resources to produce 80,000 pounds of rice: |
| |
|
| Input |
Current quantity
of input |
Price per unit
of input |
Marginal product
(pounds of rice) |
| Labor |
2000 hours |
$10 |
20 |
| Water |
100 acre-feet |
$20 |
40 |
| Land |
40 acres |
$600 |
1,500 |
|
| |
For each of the following two time horizons, indicate
whether you think the farmer is minimizing the cost of producing 80,000
pounds of rice. If so, explain why. If not, explain why not, and indicate
the direction
of a cost-reducing input adjustment: |
| |
a. |
In the short run, when the farmer can vary only
labor and water.
Yes, in the SR. See rows 1-3 in the
table below.
| |
|
Option 1: Lowest MC |
Option 2: LCC: highest
MP per dollar |
| 1 |
SR: |
Equally low MC using
either input |
Equally high extra Q per
$ using either input |
| 2 |
Labor |
$10/20 = $.50 per pound
using labor |
20/$10 = 2 extra pounds per
$ of extra labor |
| 3 |
Water |
$20/40 = $.50 per pound
using water |
40/$20 = 2 extra pounds per
$ of extra water |
| 4 |
LR: |
Lowest MC using land |
Highest extra Q per $
using land |
| 5 |
Land |
$600/1500 = $0.40 per pound
using land |
1500/$600 = 2.5 extra pounds
per $ of extra land |
|
| |
b. |
In the long run, when the farmer can vary all
three inputs.
No, not in the LR. See the table
above. The farmer should increase use of land and decrease the use of labor
and water to reduce costs.
Answer key checklist:
(1) Did you substitute land for labor and water? You shouldn't
just recommend increasing land; you should also recommend decreasing
labor and water. (2) For the lowest MC approach, were you careful with your
phrasing? For example, you should not say "the MC of land is the lowest";
you should say, "the marginal cost (of output) is lowest by
using more land instead of water or labor." The farmer is producing
rice, not land. |
| |
|
