Homework 10: key

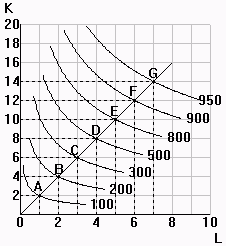
(From Frank, Chapter 9) A wag once remarked that when a certain government official moved from New York to California, the average IQ level in both states went up. Interpret this remark in the context of average-marginal relationships.
The politician's (the marginal) IQ was below the average for New York but above the average for California.

(From Frank, Chapter 9) True or false: If the marginal product is decreasing, then the average product must also be decreasing. Explain.
False. AP increases when MP is above it, regardless of whether MP is rising or falling.

(From Frank, Chapter 9) The following table provides partial information on total output, average product, and marginal product for a production function. Use relationships between these properties to complete the table:

Labor	Total product	Average product	Marginal product
0	0	0	---
1	180	180	180
2	320	160	140
3	420	140	100
4	480	120	60

4.	Suppose that the technology of the QKL Company can be summarized by the following production function: Q = 6.25·K¹L^1/2 where Q = output, K = quantity of capital, L = quantity of labor.
	a.	What kind of returns to scale characterizes QKL's production? Explain. IRTS: Cobb-Douglas production function, and exponents sum to 1.5 => output rises 1.5 times the rate of increase of inputs.
	b.	Calculate the following mathematical formulas for this production function's: (1) marginal product of labor (MPL) = 3.125^.K¹L^-1/2 (2) marginal product of capital (MPK) = 6.25^.L^1/2 (1) MPL = dQ/dL = (1/2)^.6.25^.K¹L^1/2-1 = 3.125^.K¹L^-1/2 (2) MPK = dQ/dK = 1^.6.25^.K^1-1L^1/2 = 1^.6.25^.K⁰L^1/2 = 6.25^.L^1/2
	c.	Are there diminishing marginal returns: (1) to labor? Yes (2) to capital? No Verify both answers mathematically. (Hint: Do this by taking the derivative of MPL and MPK and examining their sign.) (1) dMPL/dL = (-1/2)·3.125·K¹L^-3/2 which is < 0, so MPL falls as L rises => diminishing marginal returns to L. (2) dMPK/dK = d(6.25·L^1/2)/dK which = 0, so MPK is constant at K rises => constant marginal returns to K
	d.	By approximately what percentage does output rise: (1) If capital is increased by 10%? 10% (2) If labor is increased by 10%? 5% (3) If both capital and labor are increased by 10%? 15%

3.	(From Frank, Chapter 9) Identify the regions of increasing, constant, and decreasing returns to scale in the isoquant map to the right IRTS region(s) = C-D-E CRTS region(s) = A-B-C DRTS region(s) = E-F-G