Homework 3: Key

Based on the data from the "Elasticity review" worksheet, fill in the following table with the appropriate months and arc elasticity values (available online: Arc elasticity calculator (Excel)):

Elasticity (arc)	Month a	Month b	Value
(1) own-price elasticity of demand for American's economy class seats	2	5	(-)10
(2) income elasticity of demand for American's economy class seats.	1	3	+1.52
(3) cross-price elasticity of demand for American's economy class seats with respect to United's price on the same route	2	4	+13.39

Calculations: (1) own-price arc elasticity: |[(68-62)/65]/[(108-109)/108.5]|=10
(2) income elasticity of demand: [(70-65)/67.5]/[(2100-2000)/2050]=1.52
(3) cross-price elasticity of demand: [(70-62)/66]/[(111-110)/110.5]=13.39

2.	Indicate whether the cross-price elasticity of demand is positive or negative for each of the following pairs of items:
	a.	Tennis rackets and tennis balls: negative (complements)
	b.	Peanut butter and jelly: probably negative (complements to most people)
	c.	Hot dogs and hamburgers: positive (substitutes)

Consider the following demand for rock concert tickets: Qd = 20 - (1/4)·P

Complete the following table

	Price (P)	Quantity demanded (Qd)	Total expenditure (TE)	Point elasticity (e)
1	$80	0	$0	Infinity
2	$60	5	$300	3
3	$40	10	$400	1
4	$20	15	$300	1/3
5	$0	20	$0	0

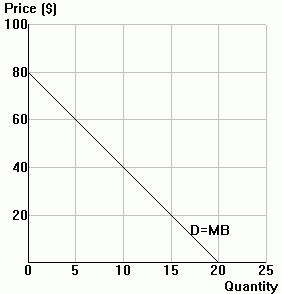Plot the demand curve in the diagram to the right. See diagram

At what price is total expenditure (TE) maximized? How does TE change with price before and after that? Are you surprised? Why or why not.
    P=$40.
    Before that price, TE rises as P falls, and after that price TE falls as P falls.
    Not surprising. P and TE move in opposite directions when demand is elastic and in the same direction when demand is inelastic.

4.	Rank from highest to lowest the absolute values of the price elasticities of demand at points A,B,C,D, and E on the three demand curves in the diagram to the right. elasticity = 1 at C,E,B; elasticity > 1 at D and A; since slope is same for both of the latter demand curves, e_D > e_A since (P/Q)_A > (P/Q)_D. So: e_D > e_A > e_C = e_E = e_B. Checklist: (1) Did you remember that e=1 halfway down a linear demand curve? (2) If you tried to make use of slope information to help rank the elasticities, did you notice that in the formula (dQ/dP)(P/Q) that the dQ/dP term is 1/slope rather than the slope itself (since Q is on the horizontal axis)?