|
Numerical
example: ? MRS formula = If Y=90 and X=30: |
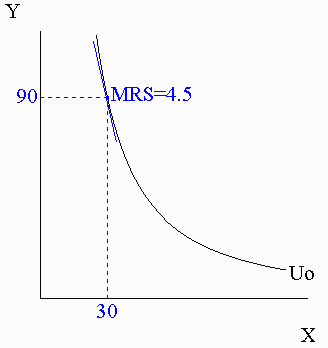 |
|
Friday, February 08, 2013 |
II. Consumer demand
A. The rational consumer
2. Consumer
preferences and indifference curves (Uo) (finish)
Ordinarily, we have smooth, convex downward-sloping
indifference curves.
For specificity, what sort of utility function would give us that
result?
One common one is...
Example: The most commonly used utility
function: Cobb-Douglas utility function:
U =
bo·XbxYby
| MUx | bx·bo·X(bx-1)Yby | bx·Y | ||||
| MRS = | -------- | = | ---------------------- | = | ------- | |
| MUy | by·bo·XbxY(by-1) | by·X |
Key result: For a Cobb-Douglas
utility function:
bx Y
MRS = ---- . ---
by X
which falls continuously as we move down an indifference
curve (X falls and Y rises).
|
Numerical
example: ? MRS formula = If Y=90 and X=30: |
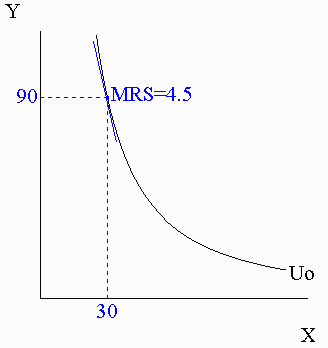 |
3. The consumer's optimum
Goal now: to combine the utility and constraint components of consumer theory to see how consumers reach an optimum, maximizing their utility given their income and price constraints.
Learning objectives: Compare relative value and cost to recommend utility-increasing consumption adjustments. Diagram and interpret the tangency condition for a consumer optimum. State and interpret the equi-marginal principle. Solve utility-maximization problems.
| Example: I = Food budget = $160 |
||
| Price | Current consumption | |
| X = Health food (H): | $2 | 40 |
| J = Junk food (J): | $1 | 80 |
| With your current consumption bundle, you are willing to trade 3J for 1H | ||
? What should you do to
maximize your utility?
a. Consume more junk food and less health food.
b. Consume less junk food and more health food.
c. Continue consuming your present quantities.
a. Comparing value and cost
Value
of 1H = 3J (<-- willing to trade 3J for 1H)
Cost of 1H = 2J (<-- PH
($2) = 2x PJ
($1)
Relative value of H > Relative price of H => hH and iJ
|
b. Geometry
Food budget = $160 ? BL equation? BLo: J = 160 - 2H Consumption point a = 40H, 80J ? MRS? MRS=3 |

|
? What does the slope of Uo tell you?
|DY/DX|Uo
= MRS = MUx/MUy = relative value of X
? What does the slope of BL tell you?
|DY/DX|BLo
= Px/Py = relative price of X
? How does relative value compare to
relative price in this case?
At point a, MRS > Px/Py
=> relative value of X > relative cost of X
=> consume more X, less Y
-> move to consumption bundles that are both affordable and
preferable.