Suppose that a cookie cafe faces the situation depicted in the diagram to the right for each of its customers.
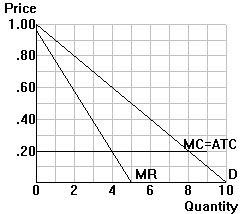
What price will maximize the firm's profits? $______
How large will its profits be? $______
How many cookies should the cafe sell? ______
|
Wednesday, April 10, 2013 |
Price discrimination worksheet
|
Suppose that a cookie cafe faces the situation depicted in the diagram to the right for each of its customers. |
 |
||
| Simple monopoly: Suppose
the cafe can charge only one price for its cookies: What price will maximize the firm's profits? $______ How large will its profits be? $______ |
|||
| 1. | First-degree price discrimination: | ||
| a. | Now suppose
that the cafe can perfectly price
discriminate by charging a different price for each additional cookie. How many cookies should the cafe sell? ______ |
||
| How much should it charge for cookie # (quit when you reach
the quantity you recommend): 1_____ 2_____ 3_____ 4_____ 5_____ 6_____ 7_____ 8_____ 9_____ 10_____? |
|||
| b. | How large will each of the following be? TR: $______ TC: $______ Profits $______ | ||
| c. | Shade in the area that corresponds to the profits earned under first-degree price discrimination. | ||
| d. | First-degree price discrimination using "two-part tariff": | ||
| Step 1: |
Produce the efficient quantity (Q*): Q* = ______ |
||
| Step 2: | Set price equal to marginal cost at Q*: Cookie price = ______ | ||
| Step 3: | Charge an access fee equal to consumer surplus at Q*: Cafe cover charge = ______ | ||
| 2. | Second-degree price discrimination: Suppose that the cafe can charge 60 cents for the first 4 cookies and 40 cents for extras beyond 4. | ||
| a. | Will the cafe's profits rise or fall compared to simple
monopoly? ______ By how much? _________ |
 |
|
| b. | Illustrate the cafe's price schedule in the diagram to the right. | ||
| c. | Shade in (1) the change in profits and (2) the change in consumer surplus compared to simple monopoly pricing. |
||
|
3. |
Third-degree price discrimination: Pasadena Car Wash has two groups of customers: adults and seniors, each with a constant price elasticity of demand. | ||||||||||
|
a. |
What is the formula for a monopoly's markup pricing
rule?
|
||||||||||
|
b. |
The marginal cost of washing each car is $4. How much should Pasadena Car Wash charge each group of customers? | ||||||||||
|
|||||||||||
| 4. | The Museum of Fine Arts (MFA) in Boston normally charges $4 for admission. Suppose that the number of MIT students who visit the MFA is given by: Q = 6000 - 1000P and that the marginal cost of additional visitors is 0. | 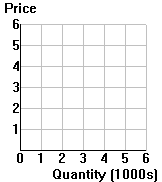 |
||||||||||||||||||||
| a. | Draw MIT's demand curve in the diagram to the right, and depict the equilibrium situation with the regular $4 admission price. | |||||||||||||||||||||
| b. | Why might it be reasonable to assume that MC=0?
|
|||||||||||||||||||||
| Consider two alternative ways of charging MIT
students for admission to the MFA: Option A: Charge the normal price of $4. Option B: Collect a lump sum payment of $10,000 from MIT (financed by MIT out of student tuition revenues) and grant MIT students free admission. |
||||||||||||||||||||||
| c. | Complete the following table comparing the two options: | |||||||||||||||||||||
|
||||||||||||||||||||||
| d. | How is it possible for Option B to make both MIT students and the MFA better off compared to Option A? | |||||||||||||||||||||