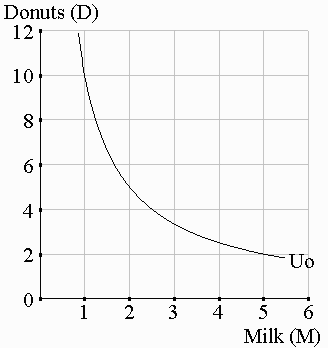
| (1) The geometry of the MRS In the diagram to the right, consider two points on Uo:
How much has each of the following changed in the move from A to B?
|
 |
|||||||||||||||
|
Wednesday, February 06, 2013 |
The Marginal Rate of Substitution (MRS)
| (1) The geometry of the MRS In the diagram to the right, consider two points on Uo:
How much has each of the following changed in the move from A to B?
|
 |
|||||||||||||||
The slope of an indifference curve is called
the marginal rate of substitution (MRS).
It tells us the rate at which good X can substitute for good Y without
affecting utility.
The MRS = the maximum amount of Y which a consumer is willing to give up to get another unit of X
(2) the mathematics of the MRS
Even though we can’t directly measure MUs, we can show that they do determine the slope of Uo:
DU = MUx.DX + MUy.DY
Along Uo, DU = 0 =>
-MUy.DY = MUx.DX =>
|-DY/DX| = MUx/MUy
(3) the logic of the MRS
| General case: | | | Example here: | |
| MUx = the utility gained from an extra X | | | MUx = 10 utils | |
| MUy = the rate that utility falls when giving up Y | | | MUy = 2 utils | |
| | | |||
| => MUx/MUy | | | 10u/(2u per Y) | |
| = total Y you can give up for 1X without losing any utility | | | 5Y for 1X | |
| = |-DY/DX| (the size of the slope of Uo) | | |