|
Friday, February 01, 2013 |
The budget line and its slope
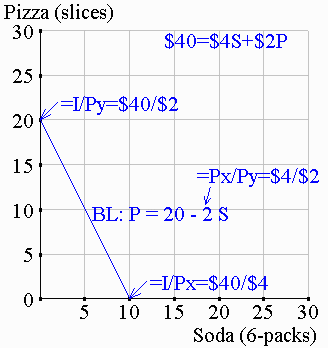
| (1) The geometry of the BL The consumer's budget constraint: Rearranging terms to express the amount of Y you can buy as a function of how much X you buy gives us the budget line (BL):
I Px In the example here, you have a $40 food budget to spend on soda ($4 per 6-pack) and pizza ($2 per slice): P = ($40/2$) - ($4/$2)·S P = 20 - 2·S |
 |
(2) the mathematics of the BL slope
DI = PxDX + PyDY
Along a BL, DI = 0 which =>
-PyDY = PxDX =>
|-DY/DX| = Px/Py.
The size of the slope of a BL = the price of X relative to Y.
(3) the logic of the BL slope
|
General case: |
| | Example here: | |
| Px = how much money you need for a unit of X. | | | Px = $4 | |
| Py = the rate you get money by giving up Y. | | | Py = $2 | |
 |
| | ||
| => Px/Py | | | $4/($2 per Y) | |
| = total Y you must give up to afford 1X (your O/C) | | | 2Y for 1X | |
| = |-DY/DX| (the size of the slope of the budget line) | | |