Marginal and average value geometry exercise

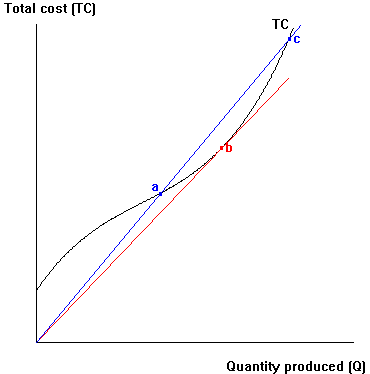
	You can examine any total value function to find the marginal and average values related  to it.     The example here shows a total cost (TC) function for a firm. When we examine it, we can see how the firm's marginal cost (MC) and average total cost (ATC) behave.
1.	Consider the three points a, b and c in the diagram, and use the notation >,<,=,? to compare values for each of the following:
	1. MCa ___ MCb	4. ATCa ___ ATCb	7. MCa ___ ATCa
	2. MCb ___ MCc	5. ATCb ___ ATCc	8. MCb ___ ATCb
	3. MCa ___ MCc	6. ATCa ___ ATCc	9. MCc ___ ATCc
2a.	Indicate approximately where in the diagram MC reverses its behavior.
2b.	Does MC (1) fall and then rise as Q rises, or (2) rise and then fall as Q rises? ____
3a.	Indicate approximately where in the diagram ATC reverses its behavior.
3b.	Does ATC (1) fall and then rise as Q rises, or (2) rise and then fall as Q rises? ____