The free trade budget line (BLf)

    The budget line: Recall from intermediate microeconomics that a budget line shows all the consumption bundles that are affordable with a given total budget and given market prices.

    The free-trade budget line (BLf): In international economics, a free-trade budget line shows the set of consumption bundles which a country can obtain by trading its output with other countries. Its two key characteristics:
    (1) it passes through the country's production point, since the country can always refuse to trade and simply consume what it produces itself, and
    (2) its slope is determined by the world price of good X relative to good Y (Px/Py).

    The slope of the free-trade budget line:
    As you move along a budget line, your change in total expenditure on good Y (DTEy) is exactly matched by an offsetting change in your total expenditure on good X (DTEx). We can use that relationship to show that the slope of budget line is determined by the price of X relative to Y. Formally:
            DTEy = -DTEx
    =>    Py·DY = -Px·DX
    =>    DY/DX = -Px/Py.
The rate at which Y exchanges for X (Dy/Dx) depends on how expensive X is relative to Y (Px/Py).
The more expensive X is relative to Y, the more Y it fetches in exchange, and vice versa.
    In terms of the geometry of the budget line, when X is expensive relative to Y, the budget line is steep (X trades for a lot of Y), and when X is cheap relative to Y, the budget line is flat (X trades for only a little Y).

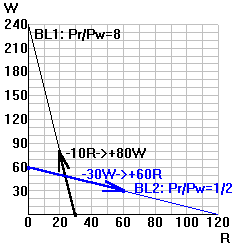    Interpreting the numerical value of the slope: The numerical value of Px/Py tells you exactly how much Y you get in exchange for exactly 1X. Consider two examples:
    Case 1: Px/Py = 8. X is 8 times as expensive as Y, so each X trades for 8Y. So if the price of Y is $10, the price of X is $80. You can export 1X for $80, which is enough to import 8Y. Or you can export 8Y and get $80 for that, which is just enough to import 1X.
    Case 2: Px/Py = 1/2. X is 1/2 as expensive as Y, so each X trades for 1/2 Y. So if the price of Y is $10, the price of X is $5. You can export 1X for $5 which is enough to import 1/2 Y. Or you can export 1/2 Y for $5, which is just enough to import 1X. (Just scale up from there for a larger volume of trade. Export 30Y, for example, and you'll be able to import 60X--the $300 you earn from exporting 30Y will exactly cover the $300 you spend importing 60X.)