Firm supply decisions under perfect competition

Suppose you have a costume firm with the cost structure given in the table below. You are a perfectly competitive firm, so you can sell as many Halloween costumes as you want at the going market price.
Part 1: Suppose that the price = $13, and the following table summarizes your revenue and cost situation:
	(1) (2) (3) (4) (5) (6) (7) (8) (9) (10) Q P TR TC TVC TFC Profit MR MC MRvsMC (>,<,=) 0 13 0 13   0 13 -13 --- --- --- 1 13 13 22 9 13 -9 13 9 > 2 13 26 27 14 13 -1 13 5 > 3 13 39 33 20 13 +6 13 6 > 4 13 52 40 27 13 +12 13 7 > 5 13 65 50 37 13 +15 13 10 > 6 13 78 63 50 13 +15 13 13 = 7 13 91 80 67 13 +11 13 17 <
	How much output should the firm produce to maximize profits? Q* = ________
Part 2: Marginal analysis helps determine the firm's profit-maximizing output (Q*) for any possible market prices:
	2.1: Expand production as long as MR > MC (the upward-sloping portion of MC). 2.2: If profits are < 0, check to be sure that TR > TVC (=> P > AVC). If not, shut down.
	(1) (2) (3) (4) (5) (6) (7) (8) (9) P=MR Q* TR TC Profit TVC AVC MC PvsAVC $17 7 119 80 +39 67 9.57 17 > 13 6 78 63 +15 50  8.33 13 > 10 5 50 50 0 37  7.40 10 > 8 4? 32 40 -8 27 6.75 7 > 7 4? 28 40 -12 27  6.75 7 > 6 3? 18 33 -15 20  6.67 6 <
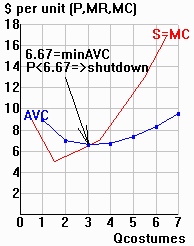
	Key lesson: The firm's supply curve = its upward-sloping MC curve above its minimum AVC (for price < minimum AVC, Qs = 0).