Consider the following total cost (TC) function we've been using a lot this term:
    TC = 196 + 147Q - 24Q² + 2Q³
where Q = 1000s of units and TC = $1000s.

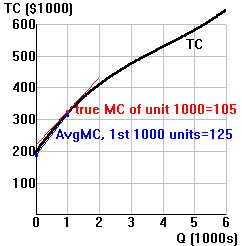
    Using the old slope method over the usual big range: If we use the old slope method of calculating MC, we actually get the average MC of output over a discrete range:

In 1,000s		In true units		Estimated MC
Quantity	Total cost	Quantity	Total cost
0	$196	0	$196,000	$321,000-$196,000   $125,000    ----------------- = -------- = $125      1,000 - 0           1,000
1	$321	1,000	$321,000

 
    Applying the old slope method to a smaller range: What we really want is a more precise estimate of the slope, to find the marginal cost of unit number 1000 itself. Continuing with the discrete method, and plugging in actual values, we would have:

In 1,000s  (true units)		MC
Quantity	Total cost
.999  (999)	$320.89498  ($320,894.98)	$321,000-$320,894.98   $105.02  -------------------- = ------- = $105.02    1,000 - 999             1
1  (1,000)	$321  ($321,000)

 
    Using the derivative: The actual derivative is MC = dTC/dQ = 147 - 48Q + 6Q². Simply plugging in Q=1 gives:
        MC at Q=1 = 105.
So notice it's a much more precise estimate of MC than the old slope method over a big range, and it gets even better as the units of measurement get larger.

Here's what it looks like: