Testing Syllogisms for Validity
Using Venn Diagrams
A syllogism, like any other type of argument is valid just in case it is not
possible for the premises to be true and the conclusion false. To test a
syllogism for validity we Venn diagram the premises and inspect the result. If
the diagram of the premises excludes the possibility of the conclusion being
false, then the syllogism is valid. In other words, if the Venn diagram of the
premises includes a representation of the conclusion, then the syllogism is
valid. Otherwise it is invalid. Since any syllogism has exactly three terms, the
Venn diagram of a syllogism will have three circles.
Although it doesn't really matter which circle represents which terms, standardly the left circle represents the minor term, the right circle represents the major term, and the bottom circle the middle term. Let's diagram our "fish" syllogism:
| All fish are swimmers. |
| All bass are fish. |
| All bass are swimmers. |
We Venn diagram the premises, one at a time, on one Venn diagram.
"All fish are swimmers" is diagrammed as follows:
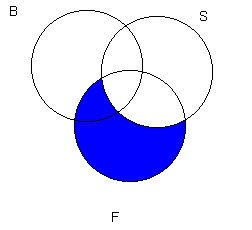
Now we add the diagram for "All bass are fish."
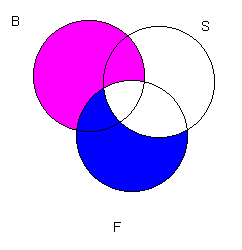
Now we ask: Does the Venn diagram contain a diagram of the conclusion? We see that it does, since the area which is in B but not in S is completely shaded. Thus the argument is valid.
Consider our dog syllogism:
| Some dogs are happy |
| Some dogs are not brown. |
|
No brown things are happy. |
Construct a Venn diagram. Does the diagram contain a diagram of the conclusion? No - that would only be the case if the common area of C and H were shaded. Thus the argument is invalid.
For this syllogism, we have two particular premises. REmember that we use "x"s to mark areas where something exists in the class represented by the subject and predicate circles. When we diagram syllogisms, we are using three cirles, and so the area where we would place our "x" is segmented into two regions. To handle this potental ambiguity, we place the "x" on the border of the two regions, to indicate that the "x" could be in either of the two regions. For example, returning to our dog syllogism, rewrite it as:
| Some D are H. |
| Some D are not B. |
|
No B are H. |
Now we diagram the first premise:
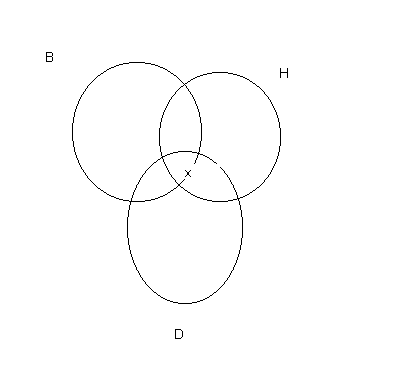
Note that the "x" is in the area that is both D and H. But it is on the border of the area that is B. It might be in B or it might not. The first premise doesn't make that clear. So we express the lack of information by placing the "x" on the line.
Now we diagram the second premise:
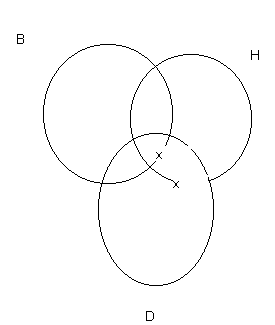
Here our "x" is in the area of D outside of B. But it is on the line of the border of H. Do we have a diagram of the conclusion, "No B are H"? Clearly not. So the argument is invalid.
Exercise: Will there be any valid syllogisms whose premises are both particular but whose conclusion is universal? Explain your answer.
Remember, when diagramming particular categorical propositions we must be careful not to represent any more content than we are given. That is why we must place our "x's" on the line and not squarely in a particular area. For example, when we diagramed "Some dogs are happy", we did not know whether the D which is H is in the C-circle or not. By putting it on the line of the C-circle we are saying, in effect, that it is either in C or it is not. To put the x in the C-circle would be to represent more than we are given by "some D are H". The same is true if we put the x outside the C-circle.
To sum up: To test a syllogism for validity, Venn diagram the premises. Inspect the diagram. If the diagram already represents the conclusion, then the argument is valid. If a representation of the conclusion is absent, the argument is invalid.