The Semantics of Categorical Sentences

We can represent the meaning of categorical sentences by using a type of diagram invented by the 19th century logician and mathematician John Venn. They are called Venn diagrams. Since a categorical sentence is a sentence about the relation of two classes of things, we use circles to represent the two classes.

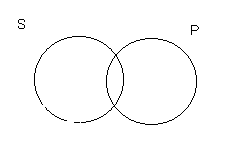
We allow the two circles to overlap, so that we can represent either the partial or full inclusion of one class in another. Whatever is inside the S circle is a member of the class of S things. Whatever is in the P circle is a member of the class of things which is P.

To represent the particular categorical sentences, we use an "x" to show that something is a member of a class.

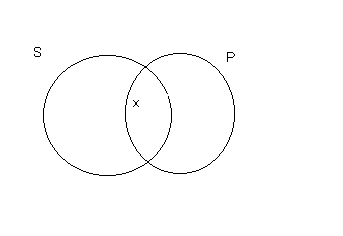
Some S are P

By placing an "x" in the overlapping area, we represent that there is something (at least one thing) which is both S and P.

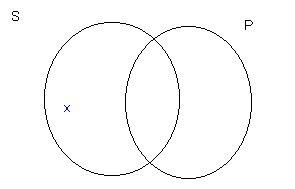
Some S are not P

Above, the area of S outside of P has at least one member. So there are some S which are not P.

To represent the universal categorical sentences we use shading to express that there is nothing in a particular class.

All S are P

The blue shading represents the area of S which is not in P, and it says that this area is empty.  So this represents the categorical sentence "All S are P".

No S are P

This Venn diagram depicts the overlapping area of S and P as emty. So it says that there is nothing which is both S and P.  Thus it represents an E, or "No S are P" proposition.