Samuel Pepys wrote Isaac Newton a long letter asking him to determine
the probabilities for a set of dice rolls related to a wager he planned
to make. Pepys asked which was more likely,
1. At least one six when six dice are rolled,
2. At least two sixes when 12 dice are rolled, or
3. At least three sixes when 18 dice are rolled.
The probability of obtaining 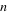 or more sixes in
a roll of or more sixes in
a roll of 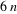 dice is given by dice is given by
where 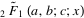 is a regularized hypergeometric function. Values for is a regularized hypergeometric function. Values for 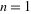 , 2, and 3 gives , 2, and 3 gives
(Sloane's A143162 and A143163).
Therefore, 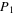 is the most likely, with is the most likely, with 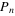 asymptotically
approaching 1/2 as asymptotically
approaching 1/2 as 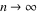 . .

Mosteller, F. "Isaac Newton Helps Samuel Pepys." Problem 19 in Fifty Challenging Problems in Probability with Solutions.
New York: Dover, pp. 19 and 33-35, 1987.
Schell, E. D. "Samuel Pepys, Isaac Newton, and Probability." Amer.
Statistician 14, 27-30, Oct. 1960.
Sloane, N. J. A. Sequences A143162 and A143163 in "The On-Line Encyclopedia of Integer Sequences."
|