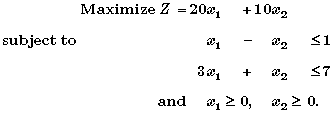
When performing algebraic procedures, it is more convenient to work with equalities than inequalities.
)
are not very convenient. (However, the nonnegativity constraints are handled
in a way that avoids the inconveniences of their inequalities.)
.| Interpretation of Slack Variables - Background | Previous | Next |
|
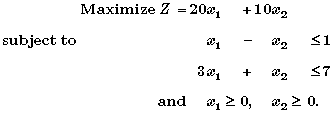| Background
When performing algebraic procedures, it is more convenient to work with equalities than inequalities. |
| Since the simplex method is an algebraic procedure, the above functional
constraints in inequality form ()
are not very convenient. (However, the nonnegativity constraints are handled
in a way that avoids the inconveniences of their inequalities.) |
| Fortunately, introducing slack variables provides a way of expressing these functional constraints as equations that are convenient for the simplex method. |
| We will begin by defining and interpreting the slack variables for the first functional constraint, |
| . |