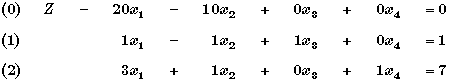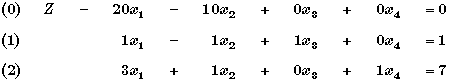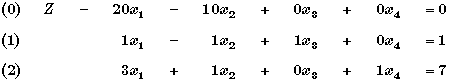 |
| The Initial Solution |
| Consider the initial system of equations exhibited above. Equations
(1)
and (2) include two more variables than
equations. Therefore, two of the variables (the nonbasic variables)
can be arbitrarily assigned a value of zero in order to obtain a specific
solution (the basic solution) for the other two variables (the basic
variables). This basic solution will be feasible if the value of each basic
variable is nonnegative. The best of the basic feasible solutions is known
to be an optimal solution, so the simplex method finds a sequence of better
and better basic feasible solutions until it finds the best one. |
To begin the simplex method, choose the slack variables to be the basic
variables, so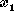 
and 
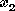are the nonbasic variables to set equal to zero. The values of 
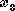and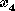 
now can be obtained from the system of equations. |
The resulting basic feasible solution is  ,  ,  ,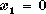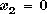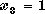
and  .
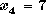Is this solution optimal? |