Jim Whitney Economics 102

Problem Set 1: Key

1. MATHEMATICAL FUNCTIONS IN ECONOMICS:
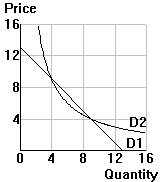
(1) b. DEMAND: Qd = B0 + B1P. B0 > 0 AND B1 < 0
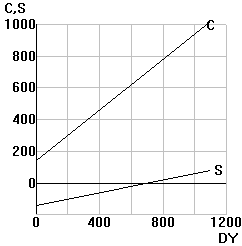
(2) e. SAVINGS FUNCTION: S = B0 + B1 DY (DY = DISPOSABLE INCOME)
B0 < 0 AND 0 < B1 < 1
(3) c. PPF: Y = B0 + B2X2. B0 > 0 AND QUADRATIC FUNCTION WITH B2 < 0
(4) d. COST FUNCTION: TC = B0 + B1Q + B2Q2 + B3Q3
B0 > 0 AND CUBIC FUNCTION WITH B3 > 0
(5) a. PRODUCTION FUNCTION: Q = B0 LB1. B0 > 0 AND 0 < B1 < 1
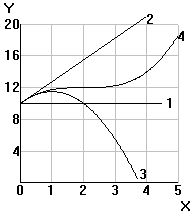
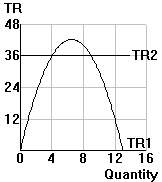
Tips: (1) Sketch the equation to see which application it looks like; or (2) point out one or more characteristics of the equation which link it to one of the applications.
whitespace.gif (816 bytes)
2. EXPLORING POLYNOMIAL FUNCTIONS:
a. x (1) (2)   (3)   (4)
0  10  10   10    10
1  10  13   11.5  11.75
2  10  16   10    12
3  10  19    5.5  12.25
4  10  22   -2    14
5  10  25  -12.5  18.75 		ps1f1.gif (2074 bytes)
b. SEE DIAGRAM TO RIGHT

 

 
c. ADDING THE POSITIVE LINEAR TERM GIVES THE FUNCTION A POSITIVE CONSTANT SLOPE. ADDING THE NEGATIVE QUADRATIC TERM PULLS THE FUNCITON DOWN AT AN INCREASING RATE, EVENTUALLY DOMINATING THE LINEAR TERM. ADDING THE POSITIVE CUBIC TERMS PULLS THE FUNCTION UP AGAIN AT AN INCREASING RATE, EVENTUALLY DOMINATING THE QUADRATIC TERM.
whitespace.gif (816 bytes)
3. CONSUMPTION AND SAVINGS:
    C = 140 + .8DY   S = -140 + .2DY ps1f1.gif (2074 bytes)
a. SEE DIAGRAM TO RIGHT
b. INTERCEPT: GIVES CONSUMPTION LEVEL IF DISPOSABLE INCOME = 0. WITH NO INCOME, THIS CONSUMPTION MUST DEPLETE SAVINGS BY AN OFFSETTING AMOUNT. SLOPE: RATE AT WHICH CONSUMPTION AND SAVINGS RISE WITH INCOME. FOR C, THIS IS CALLED THE MARGINAL PROPENSITY TO CONSUME (MPC). FOR S, THIS IS CALLED THE MARGINAL PROPENSITY TO SAVE (MPS).
c. C + S = 140 + .8DY + -140 + .2DY = DY
C+S=DY => THAT ALL PEOPLE USE ALL THEIR DISPOSABLE INCOME FOR EITHER CONSUMPTION OR SAVINGS
whitespace.gif (816 bytes)
4. CONSUMER DEMAND:
a. Complete the following table:
Quantity
baked		 Equation (1): P=13-Q Equation (2): P=36Q-1
Price Total revenue Price Total revenue
1 12 12 36 36
3 10 30 12 36
6 7 42 6 36
9 4 36 4 36
12 1 12 3 36
ps1f1.gif (2074 bytes)
b. SEE DIAGRAMS TO RIGHT ps1f1.gif (2074 bytes)
whitespace.gif (816 bytes)
5. FUNCTIONS AND SLOPES:
a. INTERCEPT = 0 ps1f1.gif (2074 bytes)
b. POWER FUNCTION
c. CONCAVE: SLOPE IS POSITIVE BUT FALLS, SO THE FUNCTION RISES, BUT AT A DECREASING RATE
d. SEE DIAGRAM, RIGHT
e. X  Y        SLOPE:
0  0
1  2          (2-0)/(1-0)=2
2  2.83    (2.83-2)/(2-1)=.83
3  3.46 (3.46-2.83)/(3-2)=.63
4  4       (4-3.46)/(4-3)=.54
Tip: One decimal point is close enough.
whitespace.gif (816 bytes)
6. INTERPRETING SLOPES IN ECONOMICS (Graders: Just correct part a.)
a. (1) (Q = f(L)): SLOPE = EXTRA OUTPUT ASSOCIATED WITH EXTRA LABOR
(2) (TC = f(Q)): SLOPE = EXTRA COST ASSOCIATED WITH EXTRA OUTPUT
(3) (PPF: Qy = f(Qx)): SLOPE = OPPORTUNITY COST OF PRODUCING MORE X
b. (1) Production functions eventually tend to become flatter as L rises BECUASE EXTRA LABOR IS PROGRESSIVELY LESS EFFECTIVE IN RAISING A FIRM'S OUTPUT AS CAPACITY IS REACHED
(2) Total cost functions eventually tend to become steeper as Q rises. SINCE LABOR BECOMES PROGRESSIVELY LESS EFFECTIVE, MORE AND MORE MUST BE USED TO PRODUCE EXTRA OUTPUT, SO COSTS BECOME PROGRESSIVELY HIGHER.
(3) PPFs tend to become steeper as Qx rises. PROGRESSIVELY HIGHER COSTS OF PRODUCTION MEAN THAT PROGRESSIVELY MORE OUTPUT ELSEWHERE MUST BE SACRIFICED TO GET MORE OF THE PRODUCT WHOSE OUTPUT IS INCREASING.
Tip: 6b is a pretty hard question. Look over the key to see if it makes sense now.