Jim Whitney Economics 250

The budget line and its slope

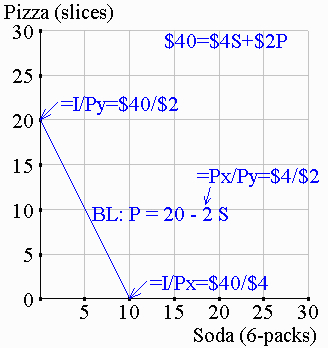
(1) The geometry of the BL

   The consumer's budget constraint:
        I = PxX + PyY.

    Rearranging terms to express the amount of Y you can buy as a function of how much X you buy gives us the budget line (BL):

             I           Px
    Y = -----  -  ------ ·X
            Py         Py

In the example here, you have a $40 food budget to spend on soda ($4 per 6-pack) and pizza ($2 per slice):

    P = ($40/2$) - ($4/$2)·S

    P = 20 - 2·S

(2) the mathematics of the BL slope

       DTE = PxDX + PyDY

        Along a BL, DTE = 0 which =>

        -PyDY = PxDX =>

        |-DY/DX| = Px/Py.

    The size of the slope of a BL = the price of X relative to Y.

(3) the logic of the BL slope

whitespace.gif (816 bytes)  whitespace.gif (816 bytes) General case: | Example here:
Px = how much money you need for a unit of X. | Px = $4
Py = the rate you get money by giving up Y. | Py = $2
whitespace.gif (816 bytes) |
=> Px/Py | $4/($2 per Y)
= total Y you must give up to raise enough money to buy 1X | 2Y for 1X
= |-DY/DX| (the size of the slope of the budget line) |