Knot Theory - Mathematics 395 - Fall 2010

1. Let D be an alternating diagram of a link L. Suppose we orient each strand in D in the direction going from its undercrossing toward its overcrossing, as in the figure below.
   
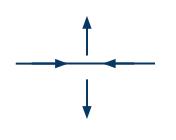
   Let C be a circle that intersects exactly 4 strands of D. Prove that as we travel along C, the 4 strands alternate between pointing into and out of C. Note: if D is a split link diagram with a separating sphere S, it may be necessary to switch all crossings on one side of S. Hint: Use induction on the number of crossings in D. (Note #2: this claim is true for any circle, not just ones that intersect D 4 times; but we don't need to prove that here.)
2. Prove that every link diagram can be turned into an alternating diagram by changing some of its crossings. Hint: Use the prvious problem, and induction on the number of crossings.